Next: Mean Value Theorem Up: Differentiation Previous: Differentiation Formnulas Contents Index
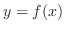 which is
which is
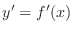 is differentiable, then we can think of
is differentiable, then we can think of
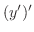 . We call this second derivative of
. We call this second derivative of 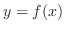 and write
and write
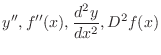
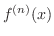 exists, we say
exists, we say  is n times differentiable
is n times differentiable
| Symbols |
|---|
3rd derivative is denoted by 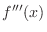 or or
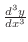 . But the 4th derivative is not denoted by . But the 4th derivative is not denoted by 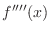 . Instead . Instead
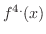 is used. is used.
|
NOTE If
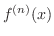 is continuous, we say
is continuous, we say  is class
is class 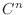 . Also, if for all
. Also, if for all  ,
,
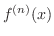 exist. Then
exist. Then  is called infinitely differentiable or class
is called infinitely differentiable or class
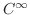 .
.
Infinitely Differentiable
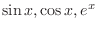 are infinitely differentiable on
are infinitely differentiable on
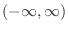 .
.
Properties of Higher Order Derivatives
 and
and 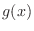 are in class
are in class 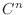 and
and 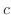 is constant. Then we have the following.
is constant. Then we have the following.
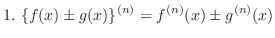
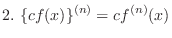
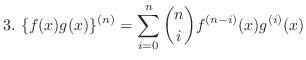
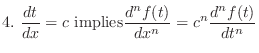
NOTE
The theorem 3. is called general Leibnitz rule.
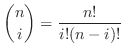
Proof of 3. Use induction on  . For
. For 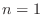 , we have
, we have
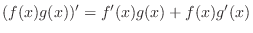
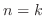 and consider for
and consider for 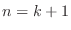 .
.
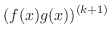 |
 |
![$\displaystyle [(f(x)g(x))^{(k)}]^{\prime} = [ \sum_{i=0}^{k}\binom{k}{i}f^{(k-i)}(x)g^{(i)}(x)]^{\prime}$](img1633.png) |
 |
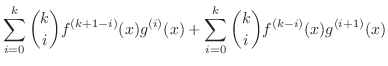 |
||
 |
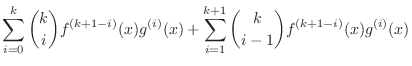 |
||
 |
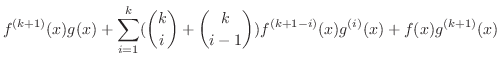 |
||
 |
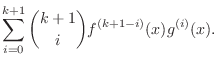 |
| Explanation |
|---|
We show why
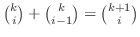 holds. We study outcomes of the case when you draw 2 balls out of box containing 5 balls. Suppose you put some mark on one of the balls. Then the number of outcomes for drawing two balls out of 4 balls is holds. We study outcomes of the case when you draw 2 balls out of box containing 5 balls. Suppose you put some mark on one of the balls. Then the number of outcomes for drawing two balls out of 4 balls is
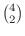 . Next, the number of outcomes for drawing two balls with one is marked is . Next, the number of outcomes for drawing two balls with one is marked is
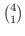 . Thus, . Thus,
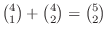 . .
|
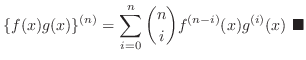
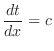 . Then
. Then
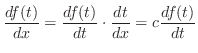 . Thus true for
. Thus true for 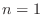 . Now assume true for
. Now assume true for 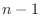 and consider for
and consider for  .
.
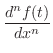 |
 |
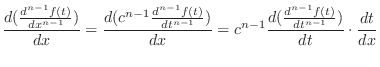 |
|
 |
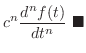 |
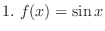
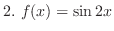
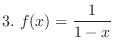
Derivatives of 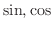 If you start at
If you start at 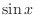 , then rotate clockwise in the picture, now you get derivative of
, then rotate clockwise in the picture, now you get derivative of 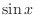 . Now note that if you add
. Now note that if you add 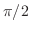 to
to 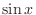 , then you get
, then you get 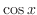 . From this observation,
. From this observation,
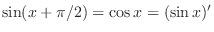
SOLUTION
1.
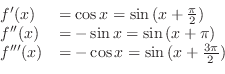
Then we can show
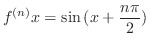 by induction
by induction

2. Let 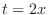 . Then
. Then
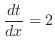 . Thus,
. Thus,
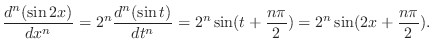
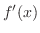 |
 |
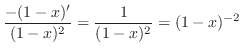 |
|
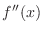 |
 |
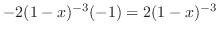 |
|
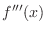 |
 |
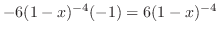 |
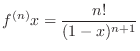 by induction
by induction

Basic Formula
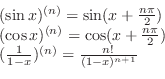
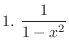
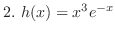
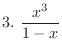
SOLUTION 1. Using the partial fraction, to write

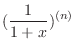 and
and
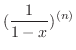 .
.
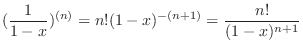
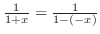 . Put
. Put 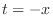 . Then
. Then
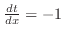 . Thus,
. Thus,
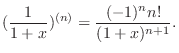
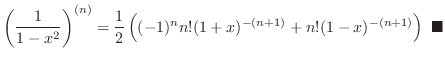
2. Note that
 . Thus we let
. Thus we let
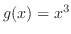 and
and
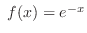 and use general Leibnitz rule,
and use general Leibnitz rule,
 |
 |
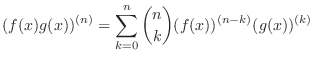 |
|
 |
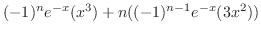 |
||
 |
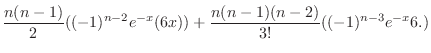 |
||
 |
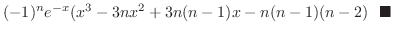 |
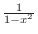 as
as
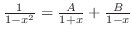 . Then clear the denominator to have
. Then clear the denominator to have
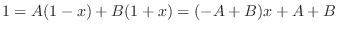 . Now this equation must be true for all
. Now this equation must be true for all  . Thus we have
. Thus we have
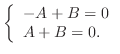 From this, we have
From this, we have
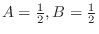 .
.
Note that  th derivative of
th derivative of 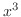 and
and 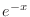 are
are
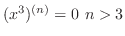 and
and
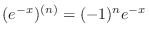 . Then, in the Leibnitz theorem, we take
. Then, in the Leibnitz theorem, we take
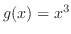 .
.
The nth derivative of 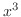 is 0 for
is 0 for 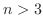 , and the nth derivative of
, and the nth derivative of
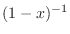 is
is
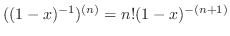 . Thus we can use general Leibnitz rule. But it is usually not good way to solve.
. Thus we can use general Leibnitz rule. But it is usually not good way to solve.
3. Since the degree of the numerator
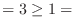 the degree of the denominator, divide the numerator by the denominator.
the degree of the denominator, divide the numerator by the denominator.
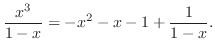
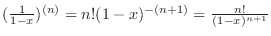 , we have
, we have
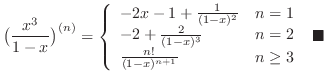
 -th derivative of the following functions.
-th derivative of the following functions.