Next: Higher Order Derivatives Up: Differentiation Previous: Derivatives Contents Index
Differentiation of Composite Functions
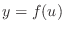 and
and 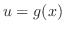 are differentiable as a function of
are differentiable as a function of 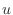 and
and  respectively, then the compostite function
respectively, then the compostite function
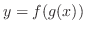 is differentiable as a function of
is differentiable as a function of  and
and
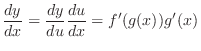
Understanding Let  be the number of plankton,
be the number of plankton, 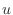 be the number of minnows, and
be the number of minnows, and  be the number of perch, then
be the number of perch, then
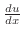 represents the rate instantaneous change of minnows against plankton. Also,
represents the rate instantaneous change of minnows against plankton. Also,
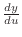 represents the rate of instantaneous change of perch againt minnows. Thus, the rate of instantaneous change of perch against plankton can be expressed by
represents the rate of instantaneous change of perch againt minnows. Thus, the rate of instantaneous change of perch against plankton can be expressed by
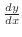 .
.
NOTE Denote 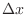 small change of
small change of  . Then
. Then 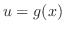 changes
changes
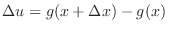 . Also,
. Also,
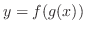 changes
changes
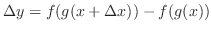 . Thus,
. Thus,
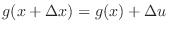 and
and
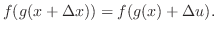
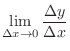 |
 |
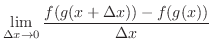 |
|
 |
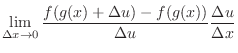 |
||
 |
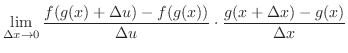 |
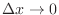 implies
implies
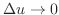 and
and
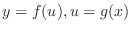 are differentiable, we have
are differentiable, we have
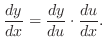
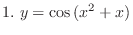
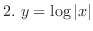 .
.
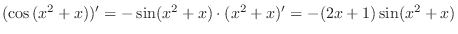 .
SOLUTION
1.
.
SOLUTION
1.
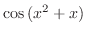 is a composite function of
is a composite function of
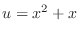 and
and
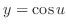 . Thus
. Thus
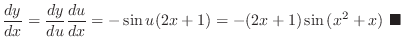
2. Suppose 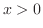 . Then
. Then
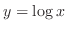 and
and
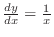 .
Suppose next that
.
Suppose next that 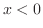 . Then
. Then 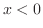 and
and 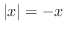 imply
imply
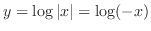 . Set
. Set 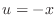 . Then ,
. Then ,
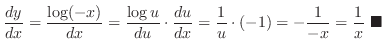
Derivative of Log
3.
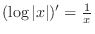
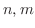 be integers. Differentiate the following
be integers. Differentiate the following
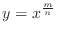
SOLUTION Raise both sides of the equation to the nth power.
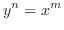
 . Then
. Then
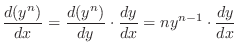
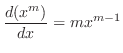
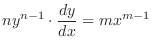
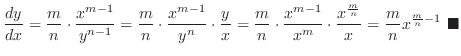
We raise both sides of equation to the nth power so that we can use
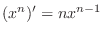 .
.
To find
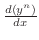 , we first differentiate with respect to
, we first differentiate with respect to  . Then
. Then
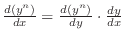 .
.
Differentiation of Inverse Function
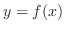 is differentiable on some interval and
is differentiable on some interval and
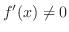 . If the inverse
. If the inverse
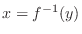 of
of 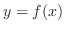 exists, then
exists, then
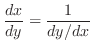
Proof
Let
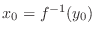 . Then
. Then
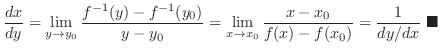
Inverse In Exercise2.4, we have found the derivative of
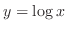 . But note that
. But note that
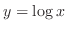 is the inverse of
is the inverse of 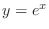 . Thus
. Thus
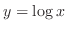 is the same as
is the same as 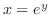 . By the theorem above, differentiate both sides by
. By the theorem above, differentiate both sides by  , we get
, we get
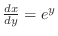 . Therefore,
. Therefore,
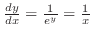 .
.
SOLUTION Note that
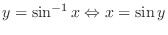 for the principal value is in
for the principal value is in
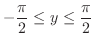 . Differentiate both sides of
. Differentiate both sides of
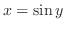 by
by  . Then
. Then
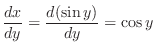
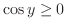 for
for
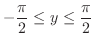 ,
,
| Derivation |
|---|
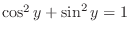 implies that implies that
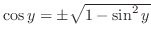 . .
|
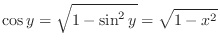
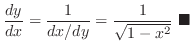
SOLUTION
Note that
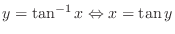 for the principal valueof
for the principal valueof
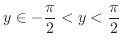 . Differentiate both sides of
. Differentiate both sides of
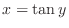 by
by  . Then
. Then
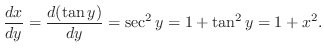
| Derivation |
|---|
Divide both side of
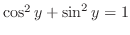 by by
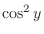 . Then we have . Then we have
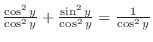 . Now write . Now write
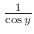 as as 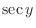 . .
|
How to read  we read
we read  as secant.
as secant.
Basic Formula
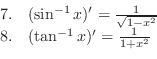
|
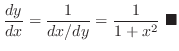
Logarithmic Differentiation
To find the derivative of
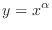 . We first take logarihtm to both sides. Then . We first take logarihtm to both sides. Then
Next differentiate both sides to get
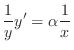
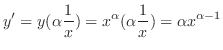
|
| Check |
|---|
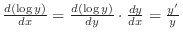 . .
|
NOTE The name logarithmic differentiation comes from this process. We also note that the derivative of
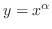 looks exactly the same as the derivative of
looks exactly the same as the derivative of 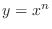 .
.
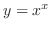 .
.
Note that the derivative of 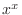 can not be derived from the basic formula. Thus we use logarithmic differentiation.
can not be derived from the basic formula. Thus we use logarithmic differentiation.
| Check |
|---|
Note that 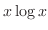 contains two contains two  's. In other words, it is a product of 's. In other words, it is a product of  and and 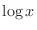 . Thus to find the derivative, we have to use the product rule. Then . Thus to find the derivative, we have to use the product rule. Then
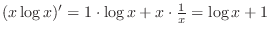 . .
|
SOLUTION Take logarithm of both sides, we have
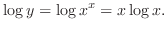
 .
.
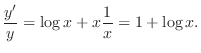
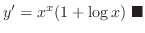
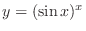 .
.
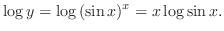
 .
.
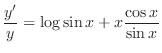

| Check |
|---|
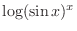 can be expressed as can be expressed as
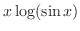 . .
Using the formula for the differentiation of inverse, 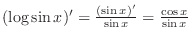 . .
|
Differentiation of Parametric Functions
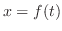 and
and 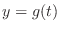 are differentiable on
are differentiable on 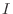 and
and
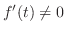 . Then
. Then  is differentiable in
is differentiable in  and the following is holds.
and the following is holds.
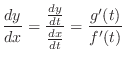
NOTE For a function 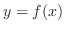 , the value of
, the value of  is determined by the value of
is determined by the value of  . If you want describe the behavior of ant on a table, you want to know the position of ant. To do this,
. If you want describe the behavior of ant on a table, you want to know the position of ant. To do this,  and
and  must be expressed using the time variable
must be expressed using the time variable 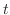 . Then we say
. Then we say 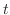 parameter. If
parameter. If  and
and  is given by
is given by 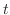 , then by the small change of
, then by the small change of 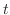 cause some change of
cause some change of  and
and  . The amount of change is given by
. The amount of change is given by 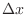 and
and 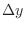 . Thus the rate of small change of
. Thus the rate of small change of  with respect to small change of
with respect to small change of  is given by
is given by
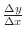 .
.
Understanding
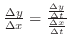 Thus the rate of infinitesimal change is given by
Thus the rate of infinitesimal change is given by
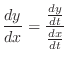
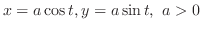 . Find
. Find
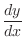 .
.
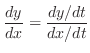
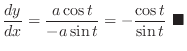
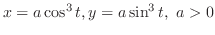 . Find
. Find
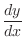 .
.
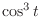
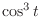 means
means
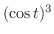 . Thus
. Thus
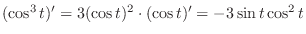 .
.
SOLUTION
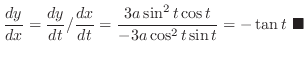
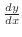
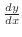 .
.