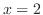Next: Differentiation Formnulas Up: Differentiation Previous: Differentiation Contents Index
On the curve defined by 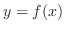 , as
, as  changes the value from
changes the value from 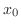 to
to 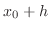 , the value of
, the value of  changes from
changes from 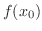 to
to
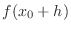 . Then the difference
. Then the difference
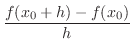
 ,
,
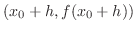 is called secant line.
is called secant line.
Difference Quotient
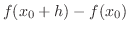 is called increment of
is called increment of  and denoted by
and denoted by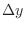 ,
,
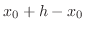 is denoted by
is denoted by 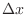 . Then
. Then
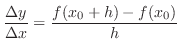
 and the increment of
and the increment of  .
Right-Hand Limit
.
Right-Hand Limit 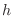 approaches 0 from the right means that the value of
approaches 0 from the right means that the value of 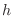 is always positive and approaches 0.
is always positive and approaches 0.
As 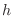 approaches 0 from the right, the secant line is getting close to the red line. Similarly, as
approaches 0 from the right, the secant line is getting close to the red line. Similarly, as 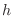 approaches 0 from the left, the secant line is getting close to the same red line. This red line is called tangent line at
approaches 0 from the left, the secant line is getting close to the same red line. This red line is called tangent line at
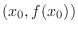 .
Differential Coefficient
Suppose that
.
Differential Coefficient
Suppose that  is defined on an interval containing
is defined on an interval containing 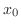 . If
. If
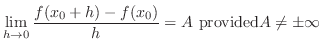
 is differentiable at
is differentiable at 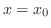 . The number
. The number 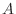 is called differntiable coefficient at
is called differntiable coefficient at 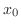 and denoted by
and denoted by
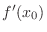 . To be differentiable, the limit
. To be differentiable, the limit  must be real number.
must be real number.
NOTE The slope of the secant line is given by
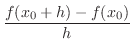
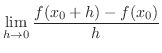
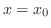 can be thought as the slope tangent line.
can be thought as the slope tangent line.
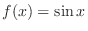 at
at 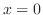 .
.
Definition
Let
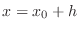 . Then we can express the differential constant in the following way.
. Then we can express the differential constant in the following way.
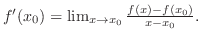
SOLUTION By the definition of differential coefficient, we have
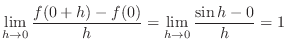
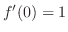

| Check |
|---|
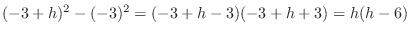 . .
|
SOLUTION By the definition of differential coefficient with
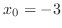 , we have
, we have
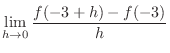 |
 |
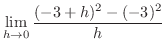 |
|
 |
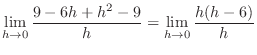 |
||
 |
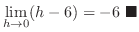 |
Equation of Tangent Line The equation of a tangent line for 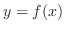 at
at
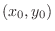 is given by
is given by
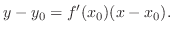
NOTE Since 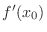 is the same as the slope of the tangent line, the slope of the line connecting two points
is the same as the slope of the tangent line, the slope of the line connecting two points 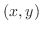 and
and
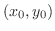 on the tangent line is equal to
on the tangent line is equal to 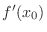 .
Equation of Normal Line A line perpendicular to a tangent line is called normal line.
The equation of a normal line to a function
.
Equation of Normal Line A line perpendicular to a tangent line is called normal line.
The equation of a normal line to a function 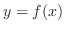 at
at
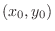 is given by
is given by
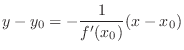
Linear Approximation The equation of a tangent line of 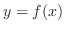 is a linear approximation. In other words, for
is a linear approximation. In other words, for
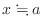 , we can approximate the value of
, we can approximate the value of  by the tangent line.
by the tangent line.
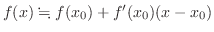 .
.
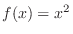 at
at 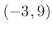 .
. 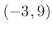 is
is
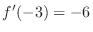 . Thus the equation of a tangent line is
. Thus the equation of a tangent line is
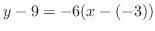
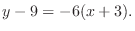
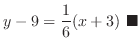
Equation of Line Consider an equation of line goes through 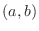 with the slope
with the slope 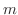 . Now take any point
. Now take any point 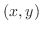 different from
different from 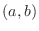 on this line. Then the slope of the line is
on this line. Then the slope of the line is
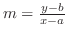 . Thus, we have
. Thus, we have
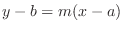 .
.
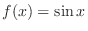 .
. 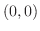 is
is 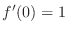 . Thus, the equation of the tangent line is
. Thus, the equation of the tangent line is
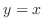
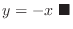
Left-Hand Differential Coefficient
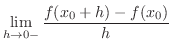
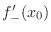 .
.
Left-Hand A left-hand differential coefficient is the same as the slope of tangent line as  approaches from the left at
approaches from the left at 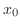 .
.
Right-Hand The right-hand differential coefficient is the same as the slope of tangent line as  approaches from the right at
approaches from the right at 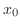 .
.
Right-Hand Differential Coefficient
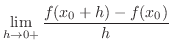
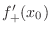 .
.
NOTE By the definition of differentiable function, if
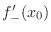 and
and
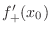 exist and their values are equal, then
exist and their values are equal, then  is differentiable at
is differentiable at 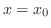 .
.
Differentiable Fcts If
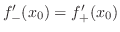 , then
, then  is differentiable at
is differentiable at 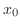 and denoted by
and denoted by
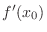 . From this, if the graph of function has sharp edge, then the function is not differentiable.
. From this, if the graph of function has sharp edge, then the function is not differentiable.
SOLUTION We need to check the left-hand differential coefficient
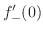 and the right-hand differential coefficient
and the right-hand differential coefficient
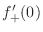 .
We first find
.
We first find
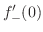 .
.
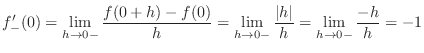
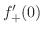 .
.
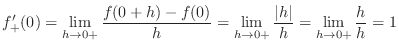
 is not differentiable at
is not differentiable at 

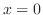 .
.
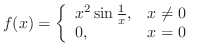
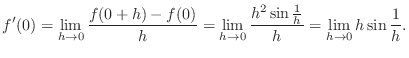
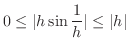
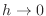 . Then
. Then
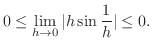
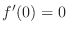 and the function is differentiable at
and the function is differentiable at 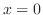

Since
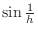 bibrates, we squeeze from the both sides. As
bibrates, we squeeze from the both sides. As
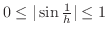 , we multiply the both sides by
, we multiply the both sides by 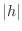 .
.
Note that
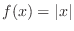 is not differentiable at
is not differentiable at 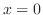 but continuous at
but continuous at 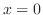 . What kind of relation can we find between differentiablility and continuity.
. What kind of relation can we find between differentiablility and continuity.
Differentiability implies Continuity
 is differentiable at
is differentiable at 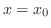 . Then
. Then  is continuous at
is continuous at 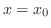 .
.
| Continuity |
|---|
 is continuous at is continuous at 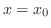 if and only if if and only if
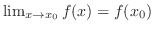 . .
|
Proof Need to show
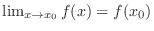 . Rewrite
. Rewrite
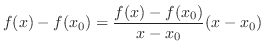
 approaches
approaches 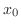 . Then
. Then
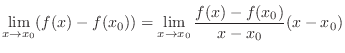
 is differentiable at
is differentiable at 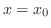 . Thus
. Thus
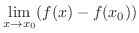 |
 |
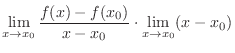 |
|
 |
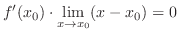 |
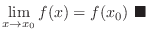
| Differentiability |
|---|
 is differentiable at is differentiable at 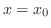 means that means that
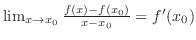 . .
|
The converse of this statement is not true. In other words, continuity does not imply differentiability. see Example2.3.
Derivatives If  is differentiable at each point on some interval
is differentiable at each point on some interval 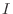 , then we say
, then we say  is differentiable on
is differentiable on 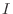 . In this case, we associate the value of
. In this case, we associate the value of  to each point in
to each point in 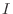 to get Derivative which is define by
to get Derivative which is define by
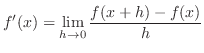
Derivatives The differentiable constant of  can be thought of the instantaneous rate of change at fixed point. On the other hand, the derivative of
can be thought of the instantaneous rate of change at fixed point. On the other hand, the derivative of  can be thought of the instantaneous rate of change at arbitrary point.
Prime Notation When we write
can be thought of the instantaneous rate of change at arbitrary point.
Prime Notation When we write 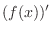 , we must differentiate with respect to
, we must differentiate with respect to  .
.
NOTE The symbols of derivatives are
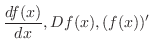
 , we say differentiate.
, we say differentiate.
SOLUTION 1.
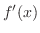 |
 |
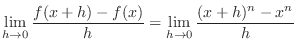 |
|
 |
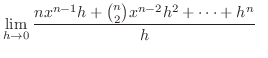 |
||
 |
![$\displaystyle nx^{n-1} + \lim_{h \rightarrow 0}[\binom{n}{2}x^{n-2}h + \binom{n}{3}x^{n-3}h^2 + \cdots + h^{n-1}]$](img1361.png) |
||
 |
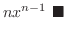 |
| Check |
|---|
To find 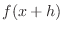 , replace , replace  by by 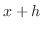 . Then we have . Then we have
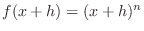 . .
|
2.
| Check |
|---|
| Using the addition formula for sine, |
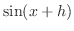 |
|||
 |
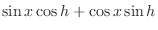 |
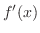 |
 |
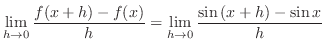 |
|
 |
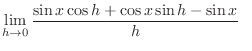 |
||
 |
![$\displaystyle \lim_{h \rightarrow 0}[\sin{x}\frac{\cos{h} - 1}{h} + \cos{x}\frac{\sin{h}}{h}]$](img1370.png) |
||
 |
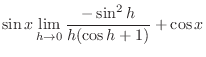 |
||
 |
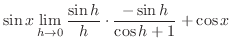 |
||
 |
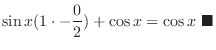 |
 |
 |
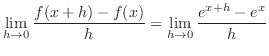 |
|
 |
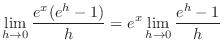 |
| Check |
|---|
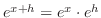 . .
|
Now let
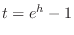 . Then since
. Then since
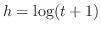 , we have
, we have
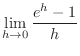 |
 |
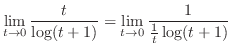 |
|
 |
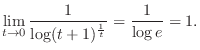 |
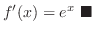
| Check |
|---|
Let
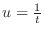 . Then . Then
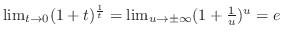 . .
|
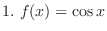
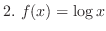
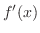 |
 |
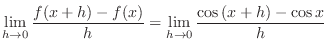 |
|
 |
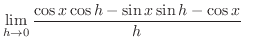 |
||
 |
![$\displaystyle \lim_{h \rightarrow 0}[\cos{x}\frac{\cos{h} - 1}{h} - \sin{x}\frac{\sin{h}}{h}] \left(\frac{\cos{h} - 1}{h} \to 0, \frac{\sin{h}}{h} \to 1\right)$](img1389.png) |
||
 |
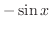 |
| Check | ||||||||
|---|---|---|---|---|---|---|---|---|
|
3. By the definition of the derivative, we have
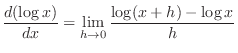
| law of logarithm |
|---|
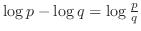
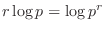 . .
|
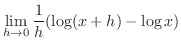 |
 |
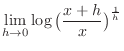 |
|
 |
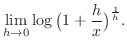 |
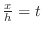 . Then as
. Then as 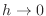 implies
implies
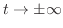 . Thus
. Thus
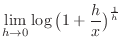 |
 |
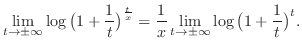 |
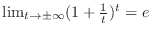 , we have
, we have
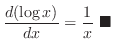
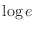 |
|---|
Note that 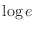 means means
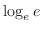 . Thus . Thus
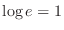 . .
|
As you saw, finding the derivative of a function by the definition is not easy. So we show useful derivative formulas.
Basic Formulas
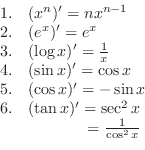
Differentiation Formula
 be differentiable and
be differentiable and  be constant
be constant
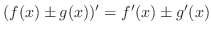
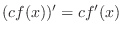
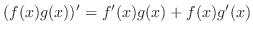
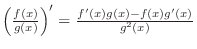
Proof
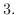 .
.
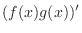 |
 |
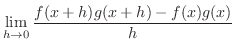 |
|
 |
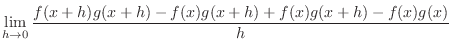 |
||
 |
 |
||
 |
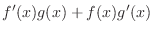 |
 Basic Technique Subtract
Basic Technique Subtract
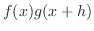 then add the same.
then add the same.
| Check |
|---|
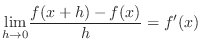
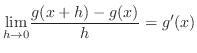 . .
|
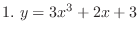
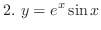
SOLUTION1.
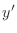 |
 |
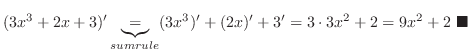 |
sum rule
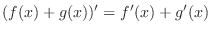
2.
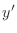 |
 |
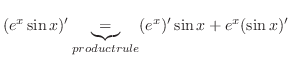 |
|
 |
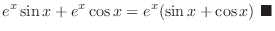 |
product rule
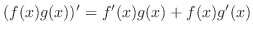
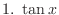
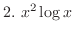
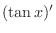 |
 |
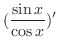 |
|
 |
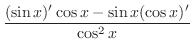 |
||
 |
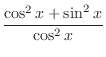 |
||
 |
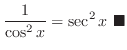 |
Quotient rule
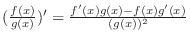
Derivative of 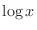 |
|---|
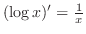 . .
|
2.
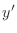 |
 |
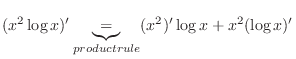 |
|
 |
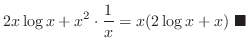 |