Next: Tangent Plane and Normal Up: Partial Differentiation Previous: Partial Derivatives Contents Index
A function
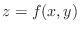 is defined on the region
is defined on the region 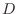 . Let
. Let
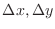 be the increment of
be the increment of 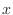 and
and 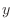 . Then
. Then
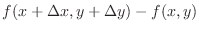 is called an increment of
is called an increment of 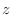 and denoted by
and denoted by 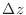 .
.
If  is partially differentiable, then
is partially differentiable, then
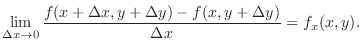
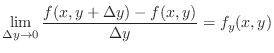
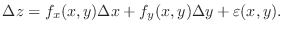
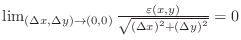 , then we say a function
, then we say a function
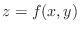 is totally diferentiable at
is totally diferentiable at 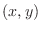
NOTE Note that we can express 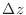 as
as
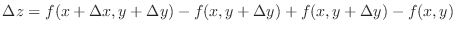
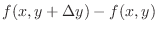 is an increment of
is an increment of 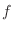 as
as 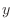 moved to
moved to
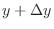 . Then we can write
. Then we can write
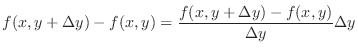
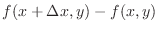 is an increment of
is an increment of 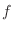 as
as 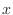 moved to
moved to
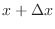 . Then we can write
. Then we can write
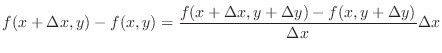
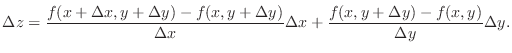
The differential of 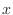 is denoted by
is denoted by 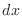 . Then for
. Then for
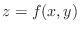 is totally differentiable at
is totally differentiable at 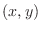 , Let
, Let
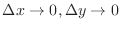 . Then
. Then
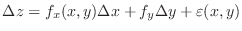 , where
, where
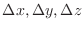 can be expressed as
can be expressed as
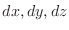 . Thus we write
. Thus we write
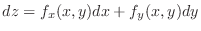
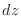 is called taltal differential of
is called taltal differential of 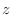 .
.
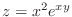 2.
2.
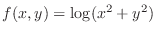 3.
3.
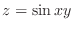
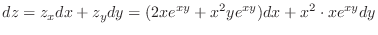
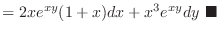
2.
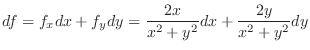

3.
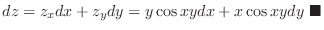
![$\displaystyle \sqrt{27}\sqrt[3]{1021}$](img346.png)
![$f(x,y) = \sqrt{x} \sqrt[3]{y} = x^{\frac{1}{2}}y^{\frac{1}{3}}$](img349.png) . Let
. Let
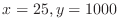 . Then
. Then
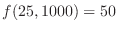 . Now let
. Now let
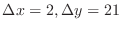 . Then
. Then
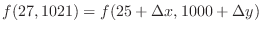 . Note that
. Note that
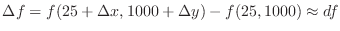 . Thus
. Thus
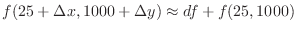
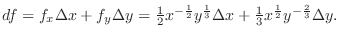 Thus for
Thus for
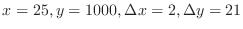 , we have
, we have
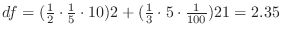 . From this,
. From this,
![$\displaystyle{\sqrt{27}\sqrt[3]{1021} \approx \sqrt{25}\sqrt[3]{1000} + 2.35 = 52.35 \ensuremath{ \blacksquare}}$](img359.png)
NOTE Suppose that  is totally differentiable at
is totally differentiable at
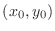 , then
, then
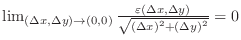 .
Now we show that
.
Now we show that  is continuous at
is continuous at 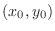 . In other words, we show
. In other words, we show
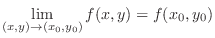
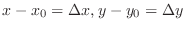 . Then
. Then
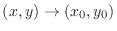 is equivalent to
is equivalent to
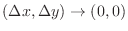 . Thus,
. Thus,
![$\displaystyle \lim_{(\Delta x, \Delta y) \rightarrow (0,0)}[f(x_{0} + \Delta x, y_{0} + \Delta y) - f(x_{0},y_{0})] = 0$](img372.png)
 is continuous at
is continuous at
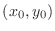 .
.
 is partially differentiable with respect to
is partially differentiable with respect to 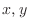 at
at 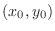 and
and 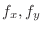 are continuous at
are continuous at 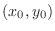 . Then
. Then  is totally differentiable at
is totally differentiable at 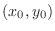 .
.
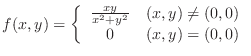
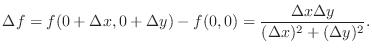 Then
Then
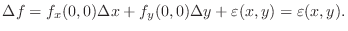 Then
Then
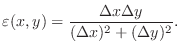
 is totally differentiable at
is totally differentiable at  only if
only if
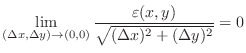
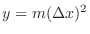 . Then
. Then
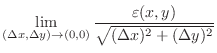 |
 |
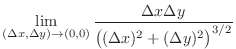 |
|
 |
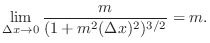 |
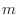 . Thus it is not totally differentiable
. Thus it is not totally differentiable
 Alernative Solution By Example4.8,
Alernative Solution By Example4.8,  is partially differentiable at
is partially differentiable at  . But by Example4.4,
. But by Example4.4,  is not continuous at
is not continuous at  . Thus by Theorem4.2,
. Thus by Theorem4.2,  is not totally diffrentiable at
is not totally diffrentiable at 

 .
.
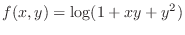
SOLUTION
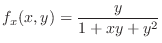 and
and
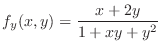 . Then
. Then
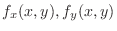 is continuous at
is continuous at  . Thus by Theorem4.3,
. Thus by Theorem4.3,  is totally differentiable at
is totally differentiable at  .
.
Altenative Solution
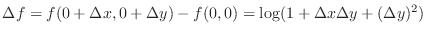 and
and
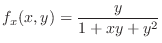 ,
,
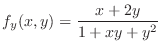 . Then
. Then
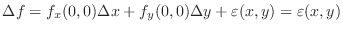
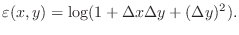 Thus,
Thus,
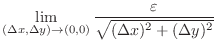 |
 |
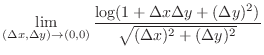 |
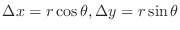 . Then
. Then
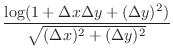 |
 |
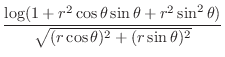 |
|
 |
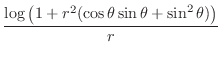 |
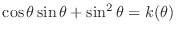 . Then
. Then
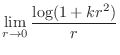 |
 |
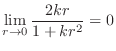 |
 is totally differentiable at
is totally differentiable at 
