Next: Partial Derivatives Up: Partial Differentiation Previous: Function of Several Variavles Contents Index
For a function
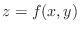 , if
, if
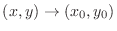 , then
, then
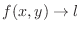 . Then we call
. Then we call 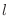 a limit of a function
a limit of a function  as
as 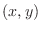 approaches
approaches
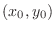 and denote
and denote
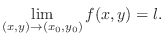
For every
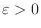 , there exists
, there exists
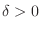 such that whenever
such that whenever
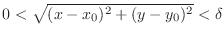 , then
, then
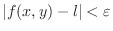 . Then
. Then
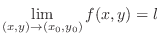
NOTE Note that
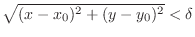 means that there are points
means that there are points 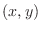 in the circle of the center
in the circle of the center
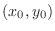 and the radius less that
and the radius less that 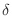 . The relation
. The relation
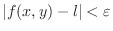 implies that the value of
implies that the value of  and
and  is very close to each other.
is very close to each other.
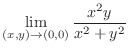
 ,
,
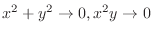 . Now we must find out which one gets close to 0 faster. To do this, we compare the least degree in
. Now we must find out which one gets close to 0 faster. To do this, we compare the least degree in 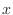 and
and 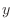 of the numerator and the denominator.
Note that the least degree in
of the numerator and the denominator.
Note that the least degree in 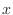 and
and 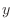 in the numerator is 3 and the least degree in
in the numerator is 3 and the least degree in 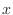 and
and 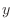 in the denominator is 2. Then we have a better chance of convergence. Thus we show that every approach to
in the denominator is 2. Then we have a better chance of convergence. Thus we show that every approach to  , we have a unique number to converge. Let
, we have a unique number to converge. Let
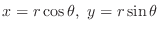

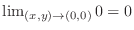 and
and
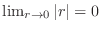 . Thus by squeezing theorem, we have
. Thus by squeezing theorem, we have
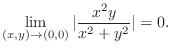
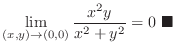
SOLUTION
Let 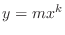 . Then we have
. Then we have
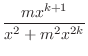 . Thus we let
. Thus we let 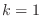 and
and 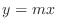 .
.
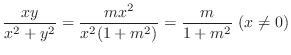
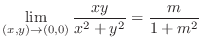
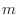 . If
. If 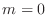 , then the limit is 0 and if
, then the limit is 0 and if 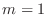 , then the limit is
, then the limit is
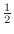 . Thus as
. Thus as
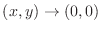 , the limit does not exist
, the limit does not exist

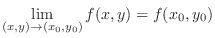
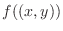 is continuous at
is continuous at
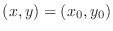 . If
. If  is continuous at all points of
is continuous at all points of
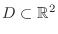 , then we say
, then we say  is continuous on
is continuous on 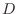 .
.
NOTE Note that  is continuous at
is continuous at 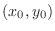 if and only if
if and only if
1.
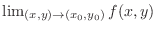 exists
exists
2.
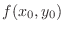 is defined
is defined
3.
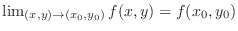
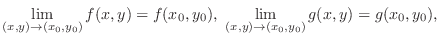
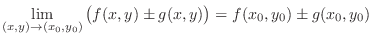
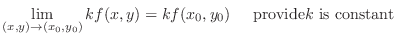
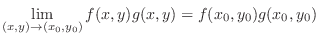
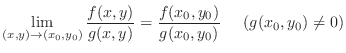
 .
.
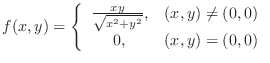
 is continuous except for the denominator is 0. Thus we only need to check continuity at
is continuous except for the denominator is 0. Thus we only need to check continuity at  . The least degree of the numerator is 2 and the least degree of the denominator is 1. Thus we let
. The least degree of the numerator is 2 and the least degree of the denominator is 1. Thus we let
 . Then
. Then
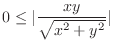 |
 |
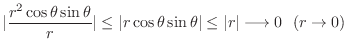 |
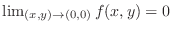 . Since
. Since
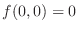 ,
,  is continuous at
is continuous at 

 .
.
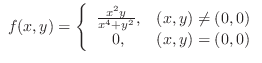
 is continuous except for the denominator is 0. Thus we only need to check continuity at
is continuous except for the denominator is 0. Thus we only need to check continuity at  . The least degree of the numerator is 3 and the least degree of
. The least degree of the numerator is 3 and the least degree of 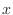 in the denominator is 4. Then we let
in the denominator is 4. Then we let 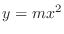 and
and
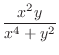 |
 |
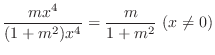 |
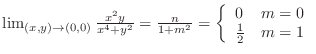 . Thus,
. Thus,  is not continuous at
is not continuous at 

Exercise A
 D
D
Exercise B
 D
D
 or notD
or notD