Next: Limit of Functions of Up: Partial Differentiation Previous: Partial Differentiation Contents Index
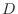 be a subset of
be a subset of
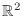 . Then for each point
. Then for each point 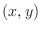 in
in 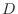 , there is a rule
, there is a rule 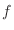 such that there exists a unique
such that there exists a unique 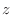 corresponding to
corresponding to 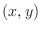 . We call this rule
. We call this rule 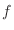 a function of two variables and denote by
a function of two variables and denote by
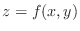 .
.
NOTE Let 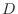 be a domian.
be a domian. 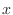 and
and 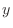 are called independent variable and
are called independent variable and 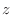 is called dependent variable. A function
is called dependent variable. A function
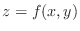 is called a function of two variables of
is called a function of two variables of 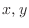 .
The domain of
.
The domain of 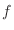 is the set of variables of
is the set of variables of 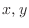 for which
for which 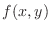 is also a real.
is also a real.
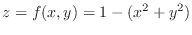
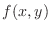 is the set of real numbers
is the set of real numbers 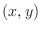 such that
such that
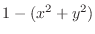 is a real number. Thus
is a real number. Thus
 |
 |
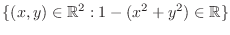 |
|
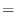 |
 |
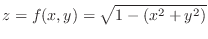
SOLUTION
Note that
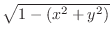 is real if and only if
is real if and only if
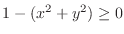 . Thus
. Thus
 |
 |
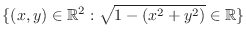 |
|
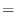 |
 |

For the function
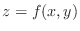 , the set of points
, the set of points 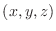 such that
such that
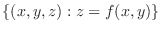 is called graph.
Thus the graph of a function of two variables is a surface.
is called graph.
Thus the graph of a function of two variables is a surface.
NOTE A surface is a collection of points. But it is not easy to draw a surface by plotting points. Then to draw the surface of a function of
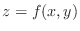 , we use the following techniques.
If we look at the surface of a function from the direction of
, we use the following techniques.
If we look at the surface of a function from the direction of 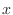 -axis, then we can only see the curve on
-axis, then we can only see the curve on 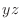 -plane.
If we look at the surface of a function from the direction of
-plane.
If we look at the surface of a function from the direction of 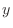 -axis, then we can only see the curve on
-axis, then we can only see the curve on 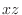 -plane.
From these observation, we can draw the surface of a function by drawing the curve of a function
-plane.
From these observation, we can draw the surface of a function by drawing the curve of a function
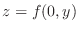 on the
on the 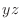 -plane and the curve of a function
-plane and the curve of a function
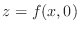 on
on 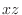 -plane.
Finally, we let
-plane.
Finally, we let 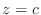 and draw the curve on the plane parallel to the
and draw the curve on the plane parallel to the 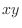 -plane.
-plane.
A line of intersection of a plane 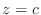 and
and
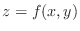 is called contour or level curve.
NOTE Let
is called contour or level curve.
NOTE Let 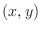 be a position of object on the
be a position of object on the 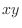 -plane and
-plane and
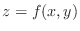 be the atomospheric pressure at the point. Then
be the atomospheric pressure at the point. Then 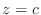 is the plane whose atomosphric pressure is
is the plane whose atomosphric pressure is 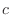 . Thus
. Thus
 is the level curve of the atomospheric pressure
is the level curve of the atomospheric pressure 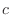 .
.
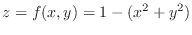
SOLUTION
Let 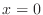 to get
to get
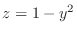 . Then we have a parabola on
. Then we have a parabola on 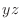 -plane. We next let
-plane. We next let 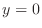 to get
to get
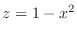 . Then we have a parabola on
. Then we have a parabola on 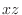 -plane. Finally let
-plane. Finally let 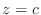 to get
to get
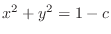 . Thus we have a circle with the radius
. Thus we have a circle with the radius
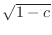 on
on 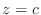

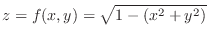 2.
2.
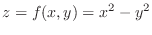 .
. 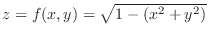 by squaring both sides to get
by squaring both sides to get
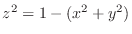 . Then htis is a sphere with the radius 1.
. Then htis is a sphere with the radius 1.
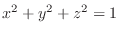 . Since
. Since 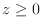 , we have upper semisphere.
, we have upper semisphere.

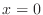 . Then
. Then
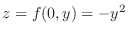 . Thus we have a concave up parabola on
. Thus we have a concave up parabola on 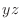 -plane. Let
-plane. Let 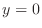 . Then
. Then
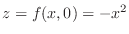 . Thus we have concave down parabola on
. Thus we have concave down parabola on 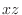 -plane. Finally let
-plane. Finally let 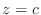 . Then we have hyperbola
. Then we have hyperbola
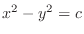 . To sketch this, imagine the saddle on a horse back
. To sketch this, imagine the saddle on a horse back

We classify the surface represented by the following quadratic equation.

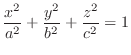
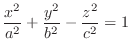
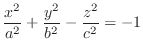
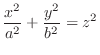
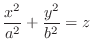
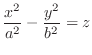
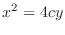

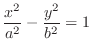
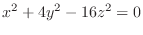 2.
2.
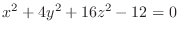
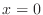 , we have
, we have
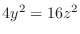 . Then
. Then
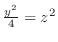 ,
,
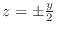 lines. Also for
lines. Also for 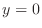 , we have
, we have
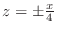 lines. Thus, it is a quadratic cone
lines. Thus, it is a quadratic cone
 2. For
2. For 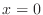 , we have
, we have
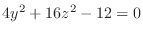 . Then
. Then
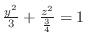 , ellipse. Also for
, ellipse. Also for 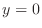 , we have
, we have
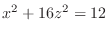 . Thus
. Thus
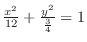 ellipse. Thus
ellipse. Thus
 , it is a ellipsoid
, it is a ellipsoid
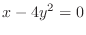 2.
2.
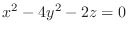
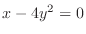 , the value of
, the value of 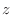 can be arbitrary. Thus we have a parabola for all
can be arbitrary. Thus we have a parabola for all 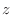 . Thus it is a parabolic cylinder
. Thus it is a parabolic cylinder
 2. Since
2. Since
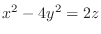 , for
, for 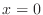 , we have
, we have 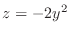 a parabola. for
a parabola. for 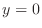 , we have
, we have
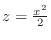 a parabola. Also for
a parabola. Also for 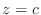 , we have
, we have
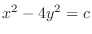 a hyperbola. Thus it is a hyperbolic paraboloid
a hyperbola. Thus it is a hyperbolic paraboloid
