Next: Total Differential and Tangent Up: Partial Differentiation Previous: Limit of Functions of Contents Index
Consider the limit of a function
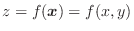 at point
at point
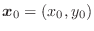 . Let
. Let 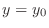 be a constant and a function
be a constant and a function
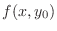 of
of 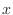 is differentiable at
is differentiable at 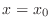 . Then
. Then
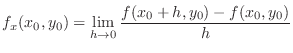
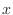 .
Similarly, Keep
.
Similarly, Keep 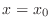 a constant and a function
a constant and a function 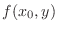 of
of 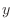 is differentiable at
is differentiable at 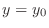 . Then
. Then
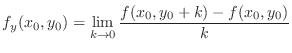
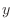 .
.
NOTE If
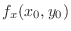 exists, then
exists, then  is called partially differentiable
with respect
is called partially differentiable
with respect 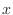 at
at 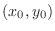 . If
. If  is differentiable at esch
is differentiable at esch 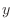 in
in 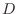 , then
, then  is called partially differentiable on
is called partially differentiable on 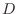 with respect
with respect 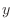 .
.
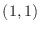 .
.
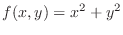
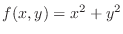 by the plane
by the plane 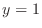 , it is enough to consider
, it is enough to consider
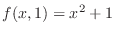 . Now differentiate
. Now differentiate 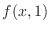 by
by 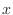 . Then we have
. Then we have
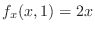 . Thus,
. Thus,
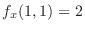

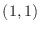 .
.
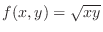
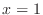 . Then slice the surface
. Then slice the surface
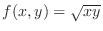 by the plane
by the plane 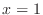 to get the curve
to get the curve
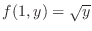 . Now differentiate
. Now differentiate 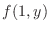 with respect to
with respect to 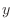 to obtain
to obtain
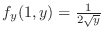 . Thus,
. Thus,
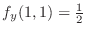

A partial derivative of  with respect to
with respect to 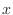 is the derivative of
is the derivative of  by keeping
by keeping 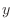 as constant. More precisely,
as constant. More precisely,
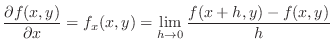
 with respect to
with respect to 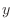 is
is
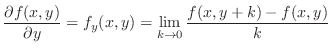
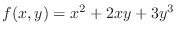 2.
2.
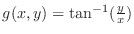
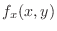 , treat
, treat 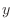 as constant and differentiate
as constant and differentiate  with respect ot
with respect ot 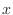 .
.
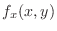 |
 |
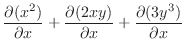 |
|
 |
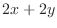 |
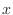 as constant and differentiate with respect to
as constant and differentiate with respect to 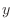
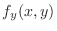 |
 |
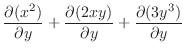 |
|
 |
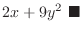 |
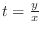 . Then
. Then
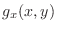 |
 |
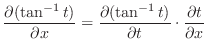 |
|
 |
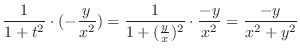 |
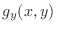 |
 |
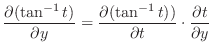 |
|
 |
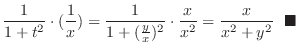 |
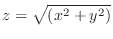 2.
2.
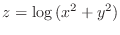
SOLUTION
1. Let
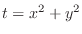 . Then
. Then
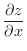 |
 |
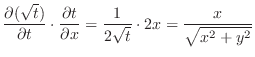 |
|
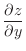 |
 |
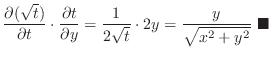 |
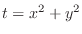 . Then
. Then
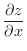 |
 |
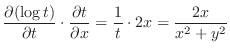 |
|
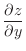 |
 |
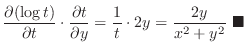 |
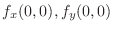 . Then determine the following function is partially differentiable with respect to
. Then determine the following function is partially differentiable with respect to 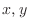 or not.
or not.
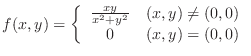
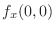 , substitute
, substitute 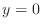 and find
and find 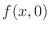 . Then
. Then
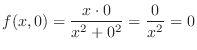
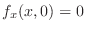 . Thus,
. Thus,
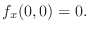
Since
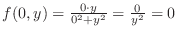 , we have
, we have
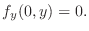 Thus
Thus
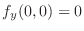 .
.
Therefore,  is partially differentiable with respect to
is partially differentiable with respect to 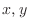 at
at 

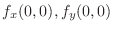 . Then determine the following function is partially differentiable with respect to
. Then determine the following function is partially differentiable with respect to 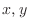 or not.
or not.
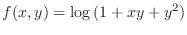
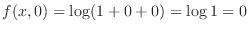 ,
,
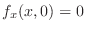 and
and
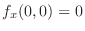 .
.
Note that
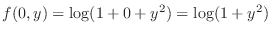 . Thus
. Thus
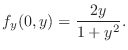
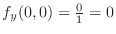 . Thus
. Thus  is partially differentiable with respect to
is partially differentiable with respect to 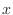 and
and 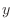 at
at 

Exercise
Exercise B