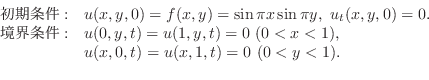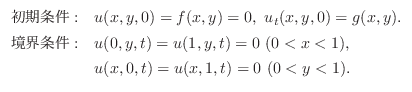演習問題7.3.2

1.

次の境界値問題を解け．

(a)

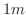両端が固定された長さ$1m$の水平に張られた弾性弦の初期形状が 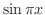$\sin{\pi x}$で与えられている．弦の初速度が0のとき，この弦の垂直方向の変位を変数分離法を用いて求めよ．

(b)

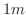両端が固定された長さ$1m$の水平に張られた弾性弦に初速度 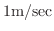$1{\rm m/sec}$を与えたとき，この弦の垂直方向の変位を変数分離法を用いて求めよ．

2.

D'Alembert法は非有限区間での波動方程式にも用いることができ

$$u(x,t) = \frac{1}{2}[f(x+ct) + f(x-ct)] + \frac{1}{2c}\int_{x-ct}^{x+ct}g(\tau)d\tau$$

は次の初期値問題の解であることを示せ．

$$u_{tt} = c^{2}u_{xx} (-\infty < x < \infty, t > 0 ),$$

$$u(x,0) = f(x), u_{t}(x,0) = g(x).$$

3.

2の結果を用いて次の初期値問題を解け．

$$u_{tt} = c^{2}u_{xx} (-\infty < x < \infty, t > 0 ),$$

$$u(x,0) = e^{-x^{2}}, u_{t}(x,0) = 1.$$

4.

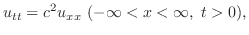
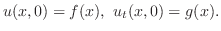
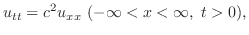
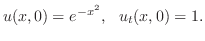
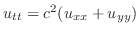2次元波動方程式 $u_{tt} = c^{2}(u_{xx} + u_{yy})$を次の条件の元で解け．

(a)

$$\begin{array}{ll} \mbox{初期条件} :& u(x,y,0) = f(x,y)= \sin{\pi ... ...< 1), \\ & u(x,0,t) = u(x,1,t) = 0 (0 < y < 1) . \end{array}$$

(b)

$\begin{array}{ll} \mbox{初期条件} :& u(x,y,0) = f(x,y)= 0, u_{t}(x,y,0) = g(x,y).... ...t) = 0 (0 < x < 1), \\ & u(x,0,t) = u(x,1,t) = 0 (0 < y < 1). \end{array}$