Next: 索引 Up: 応用数学入門 Previous: 演習問題8.2 目次 索引

1.1
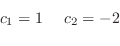
1.2
1.
2.
3.
1.3
1.
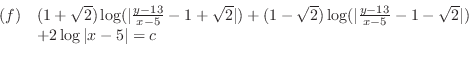
2.
例題1.9は
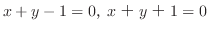 と2つの平行な直線となるため,座標軸の平行移動では定数項を落とすことができない.
と2つの平行な直線となるため,座標軸の平行移動では定数項を落とすことができない.
1.4
1.
2.
1.5
1.
2.
1.6
1.
2.
1.7
1.
2.
3.
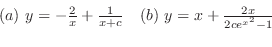
1.8
1. 省略
2.

2.1
1.
2.
3.
2.2
1.
2. 省略
2.3
1.
2.
3.
2.4
1.
2.5
1.
2. 省略
2.6
1.

3.1
1.
3.2
1.
3.3
1.
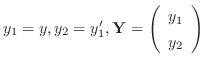 とおくと
とおくと
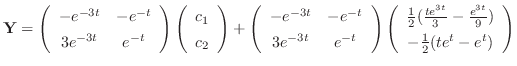
3.

4.1
1.
2.
| (a) |
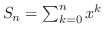 とおくと とおくと
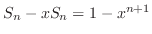 .よって .よって
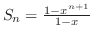 . . |
これより
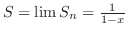 . . |
3.
| (a) |
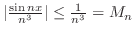 とおくと, とおくと, |
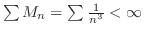 |
|
| よってWeierstrassのM-testにより一様収束. | |
| (b) |
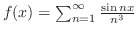 とおくと とおくと
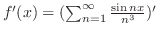 ここで(a)より
ここで(a)より |
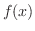 は一様収束するので項別微分が可能。よって は一様収束するので項別微分が可能。よって |
|
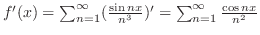 |
|
| (c) |
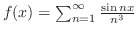 とおくと とおくと
|
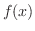 は一様収束するので項別積分が可能。よって は一様収束するので項別積分が可能。よって |
|
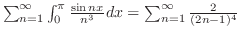 |
4.2
1.
| (a) |
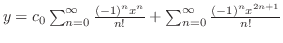 = =
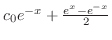 |
| (b) |
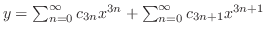 ただし ただし |
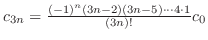 , , |
|
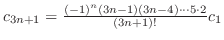 |
|
| (c) |
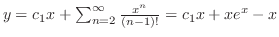 |
| (d) |
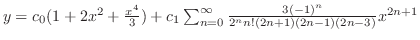 |
2.
| (a) |
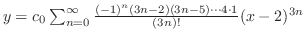 |
+
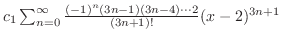 |
|
| (b) |
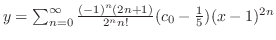 |
+
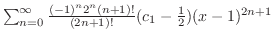 |
4.3
1.
(a) 確定特異点 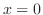 , , |
(b) 確定特異点 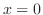 ,不確定特異点 ,不確定特異点 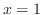 |
(c) 確定特異点 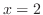 |
2.
3.

5.1
1.
5.2
1.
5.3.1
1.
5.3.2
1.
5.4
1.
5.5
1.
5.6
1.

6.1
1.
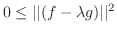 |
 |
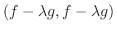 |
|
 |
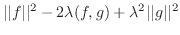 |
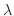 についての二次式で0より大きいので,その判別式
についての二次式で0より大きいので,その判別式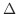 は0以下になる.よって
は0以下になる.よって
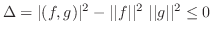
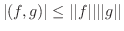
3.
6.2
6.3
1.
2.
3.
6.4
1.

7.1
1.
| (a) |
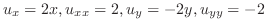 より より
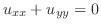 . . |
| (b) |
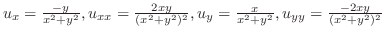 |
より
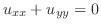 . . |
|
| (c) |
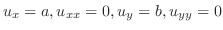 より より
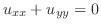 . . |
| (d) |
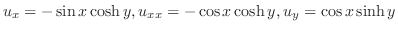 , , |
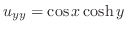 より より
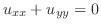 |
2.
| (a) |
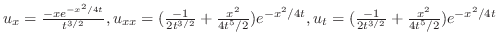 |
より
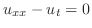 . . |
|
| (b) |
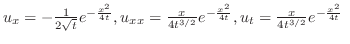 より より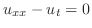 |
| (c) |
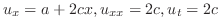 より より
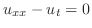 . . |
| (d) |
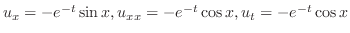 より より
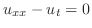 . . |
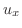 |
 |
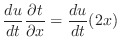 |
|
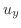 |
 |
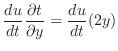 |
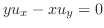 .
.
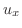 |
 |
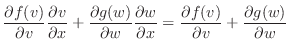 |
|
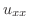 |
 |
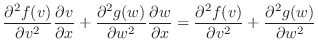 |
|
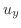 |
 |
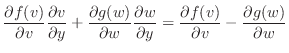 |
|
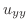 |
 |
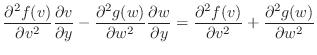 |
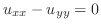 .
.
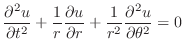
7.2
1.
2.
3.
7.3.1
2.
| (a) |
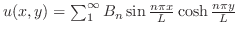 |
ただし
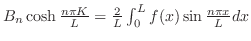 |
|
| (b) |
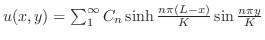 |
ただし
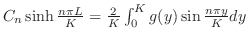 |
7.3.2
1.
4.
(a)
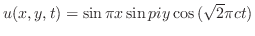 |
(b)
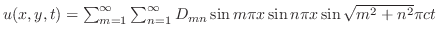 , , |
ただし
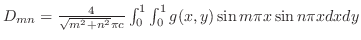 |
7.3.3

8.1
1.
2.
3.
(a)
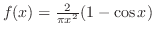 (b) 省略 (b) 省略 |
8.2