Next: 演習問題7.3.3 Up: 3つの境界値問題(Three boundary value problems) Previous: 演習問題7.3.2 目次 索引
 ,時刻
,時刻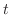 での棒の温度
での棒の温度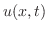 が満たす偏微分方程式について考えてみましょう.
が満たす偏微分方程式について考えてみましょう.
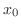 での切断面を通して
での切断面を通して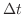 時間に棒に流入してくる熱量は,温度勾配
時間に棒に流入してくる熱量は,温度勾配
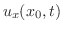 に比例するので
に比例するので
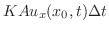 (K : 熱伝導率, A : 断面積).同じく
(K : 熱伝導率, A : 断面積).同じく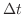 時間に
時間に
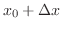 での切断面を通して流入する熱量は
での切断面を通して流入する熱量は
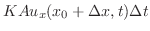 .よって
.よって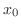 と
と
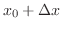 の間に流入する総熱量は
の間に流入する総熱量は
![$\displaystyle KA[u_{x}(x_{0}+\Delta x,t) - u_{x}(x_{0},t)] \Delta t $](img2256.png)
一方,この棒の比熱を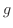 (単位質量の温度を単位時間に
(単位質量の温度を単位時間に
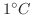 上げるのに必要な熱量)とするとき,質量
上げるのに必要な熱量)とするとき,質量
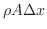 の部分が温度変化
の部分が温度変化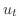 をもたらすための熱量を
をもたらすための熱量を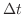 時間与えると,総熱量は
時間与えると,総熱量は
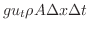
![$\displaystyle KA[u_{x}(x_{0}+\Delta x,t) - u_{x}(x_{0},t)] \Delta t = g u_{t} \rho A \Delta x \Delta t .$](img2262.png)
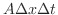 で割ると
で割ると
![$\displaystyle K[\frac{u_{x}(x_{0}+\Delta x,t) - u_{x}(x_{0},t)}{\Delta x}] = g \rho u_{t}. $](img2264.png)
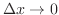 とすると
とすると
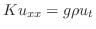
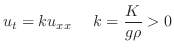
これは一次元熱伝導方程式(one dimensional heat equation)とよばれます.
外部から熱の供給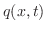 がある場合には,棒の温度
がある場合には,棒の温度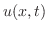 は次の式を満たします.
は次の式を満たします.
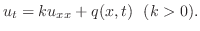
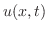 が時間
が時間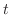 に対して一定のとき,つまり
に対して一定のとき,つまり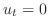 のとき,
のとき,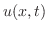 は定常状態(steady state)での温度分布を表わします.
初期条件は,定常状態での温度分布の
は定常状態(steady state)での温度分布を表わします.
初期条件は,定常状態での温度分布の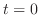 における温度分布
における温度分布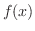 を表わします.つまり,
を表わします.つまり,
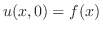
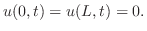
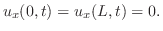
薄い板の熱伝導現象は,この板が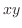 平面におかれ,時刻
平面におかれ,時刻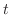 での点
での点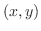 の温度が
の温度が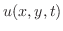 であるとき,次
の二次元熱伝導方程式(two dimensional heat equation)で表わされます.
であるとき,次
の二次元熱伝導方程式(two dimensional heat equation)で表わされます.
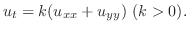
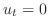 のとき,つまり
のとき,つまり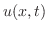 が時間
が時間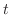 に対して定数のとき,Laplace方程式
に対して定数のとき,Laplace方程式
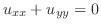 を得ます.そしてこの方程式は定常状態での温度分布を表わします.
を得ます.そしてこの方程式は定常状態での温度分布を表わします.
また円柱の熱伝導方程式は,時刻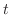 での点
での点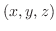 の温度が
の温度が
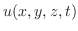 であるとき,次
の三次元熱伝導方程式(three dimensional heat equation)で表わされます.
であるとき,次
の三次元熱伝導方程式(three dimensional heat equation)で表わされます.
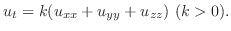
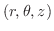 で表わすと,変数変換
で表わすと,変数変換
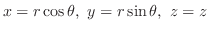
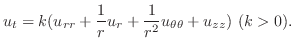
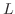 の細長い均質な棒で棒の両端の温度が0度に保たれていて,初期温度分布が
の細長い均質な棒で棒の両端の温度が0度に保たれていて,初期温度分布が
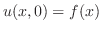 で与えられているとき棒の温度
で与えられているとき棒の温度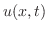 を求めよ.
を求めよ.
解 この関数の数学的モデルは熱伝導方程式
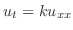
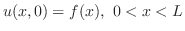 ,境界条件
,境界条件
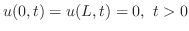 で与えられる.
で与えられる.
変数分離解
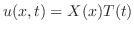 を仮定して,これを熱伝導方程式に代入すると
を仮定して,これを熱伝導方程式に代入すると
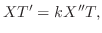
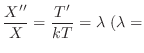 定数
定数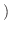
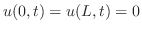 より,Sturn-Liouville問題
より,Sturn-Liouville問題
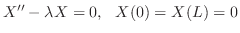
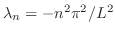 ,固有関数
,固有関数
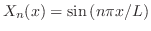 をもつ.またこの
をもつ.またこの
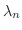 に対して
に対して
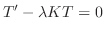 は
は
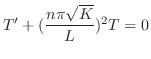
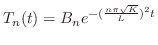
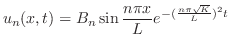
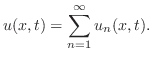
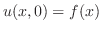 を用いると
を用いると
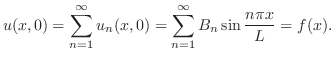
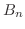 は
は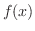 のフーリエ正弦級数の係数となるので
のフーリエ正弦級数の係数となるので
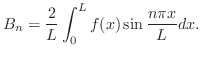
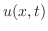 |
 |
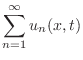 |
|
 |
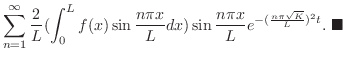 |
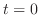 の前に棒の一端が沸騰しているお湯につけられていて,
の前に棒の一端が沸騰しているお湯につけられていて,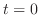 で
で
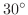 の水につけたとする.このとき棒の温度
の水につけたとする.このとき棒の温度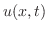 を求めよ.
を求めよ.
解 時刻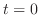 の前で,定常状態という条件のもとでは,温度分布はラプラス方程式
の前で,定常状態という条件のもとでは,温度分布はラプラス方程式
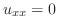 と境界条件
と境界条件
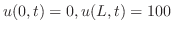 で与えられる.ここで,
で与えられる.ここで,
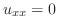 より,解を
より,解を
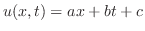 とおくと,
とおくと,
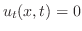 より
より
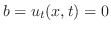 .また,境界条件より,
.また,境界条件より,
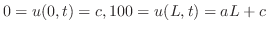 .したがって,
.したがって,
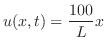
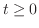 において,次の境界値問題を解くことになる.
において,次の境界値問題を解くことになる.
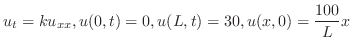
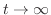 のとき
のとき
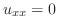 を満たす関数を考える.このような解を
を満たす関数を考える.このような解を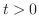 における定常状態での解といい,
における定常状態での解といい,
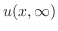 で表す.
で表す.
この解は,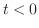 での
での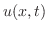 と同様にして求めることができ,
と同様にして求めることができ,
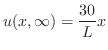
ここで,
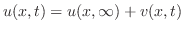 とおくと,
とおくと,
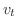 |
 |
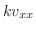 |
|
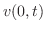 |
 |
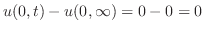 |
|
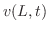 |
 |
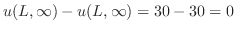 |
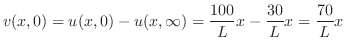
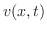 は,上の例題の
は,上の例題の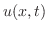 と同じで,
と同じで,
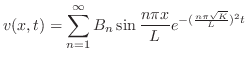
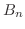 は初期温度分布関数のフーリエ正弦係数である.したがって,
は初期温度分布関数のフーリエ正弦係数である.したがって,
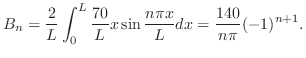
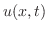 は定常状態
は定常状態
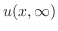 と非定常分布
と非定常分布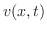 により求まることが分かる.
により求まることが分かる.

非三角関数解 三角関数は常に境界値問題の解を表すことができるとは限らない.
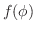 で与えられる半径1の球の内部の定常状態での温度を求めよ.
で与えられる半径1の球の内部の定常状態での温度を求めよ.
解 空間では,定常状態温度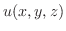 はラプラス方程式
はラプラス方程式
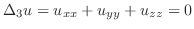 を満たす.極座標変換
を満たす.極座標変換
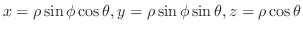
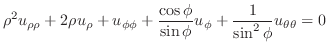
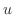 は
は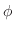 と
と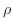 の関数のはずである.したがって,
の関数のはずである.したがって,
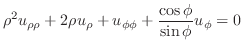
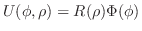 とおくと,
とおくと,
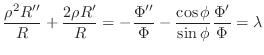
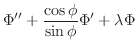 |
 |
0 | |
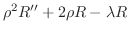 |
 |
0 |
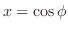 とおくと,
とおくと,
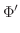 |
 |
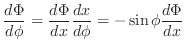 |
|
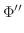 |
 |
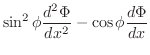 |
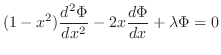
![$x \in [-1,1]$](img2343.png) で有界な解は,
で有界な解は,
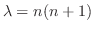 ,
,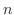 整数のときだけである.2つ目の式は,Cauchy-Eulerの方程式で,
整数のときだけである.2つ目の式は,Cauchy-Eulerの方程式で,
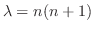 のとき,完全解
のとき,完全解
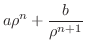
もし,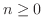 ならば,
ならば,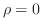 のとき意味を持つために
のとき意味を持つために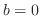 とおく.この段階で,次の解を持つ.
とおく.この段階で,次の解を持つ.
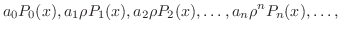
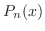 は位数
は位数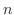 のLegendre多項式である.重ね合わせの原理より,
のLegendre多項式である.重ね合わせの原理より,
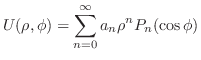
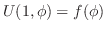 ,または
,または
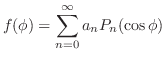
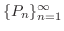 を直交系とする
を直交系とする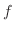 のフーリエ級数である.また,例題6.13より,
のフーリエ級数である.また,例題6.13より,
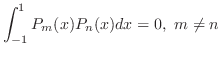
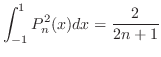
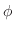 を用いて表すと,
を用いて表すと,
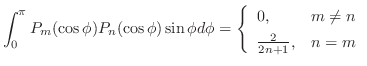
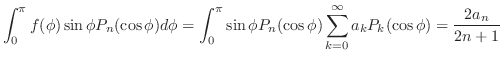
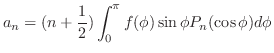

扱う領域が有界でないとき,フーリエ級数を用いて解を表わすことは不可能になります.このような場合,よく用いられるのが変換です.次の章でフーリエ変換を用いて,領域が有界でない場合の熱伝導方程式を解きます.