Next: コーシーの積分定理(Cauchy's integral theorem) Up: 複素積分 Previous: 線積分とグリーンの定理(Line integral and Green's 索引
 平面上の曲線
平面上の曲線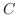 を含む領域を
を含む領域を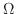 とし,
とし, を
を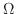 で定義された連続関数とする.
で定義された連続関数とする.
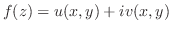
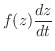 |
 |
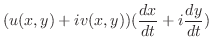 |
|
 |
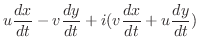 |
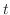 の関数であるが,積分
の関数であるが,積分
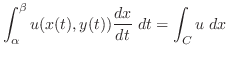
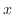 に関する曲線
に関する曲線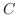 に沿っての関数
に沿っての関数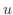 の線積分である.残りの項についても同様に考えると,次の積分
の線積分である.残りの項についても同様に考えると,次の積分
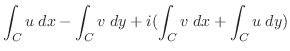
 の曲線
の曲線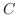 に沿っての積分といい,
に沿っての積分といい,
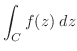
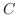 に沿って
に沿って
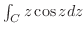 を求めよ.
を求めよ.
2 関数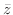 を点
を点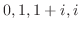 を頂点とする正方形の辺および対角線に沿って0から
を頂点とする正方形の辺および対角線に沿って0から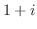 まで積分せよ.
まで積分せよ.