Next: 4.4 コーシーの積分表示 Up: 演習問題詳解 Previous: 4.2 複素積分 索引
1.
(a) 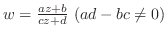 点から出発し,
点から出発し, 点に到達する曲線を
点に到達する曲線を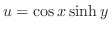 とすると,
とすると,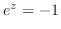 点と
点と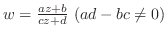 点を結ぶ曲線は
点を結ぶ曲線は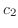 と表せる.
と表せる.

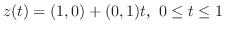 とおくと,曲線
とおくと,曲線 は領域
は領域 に含まれる閉曲線である.ここで,コーシーの積分定理を用いると
に含まれる閉曲線である.ここで,コーシーの積分定理を用いると
| 0 |  |
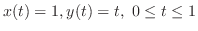 |
|
 |
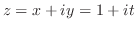 |
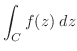
(b) まず,曲線を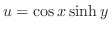 から曲線は
から曲線は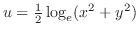 に橋をかける.次に曲線
に橋をかける.次に曲線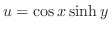 に沿って回りながら,橋を渡って曲線
に沿って回りながら,橋を渡って曲線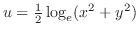 に移り,逆回りをし,元の橋を渡って曲線
に移り,逆回りをし,元の橋を渡って曲線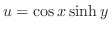 に戻り一周する曲線を
に戻り一周する曲線を とする.このとき,
とする.このとき, は領域
は領域 に含まれる閉曲線となるので,コーシーの積分定理を用いると
に含まれる閉曲線となるので,コーシーの積分定理を用いると
| 0 |  |
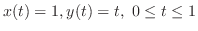 |
|
 |
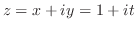 |
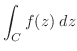
曲線 は原点を中心とする半径
は原点を中心とする半径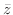 の円周であるので,
の円周であるので,
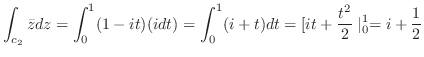 はこの円内で正則ではない.そこで,
はこの円内で正則ではない.そこで,
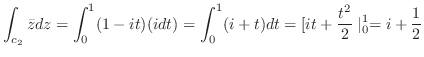 を部分分数分解すると
を部分分数分解すると
![$\displaystyle \frac{1}{z^2 + 1} = \frac{1}{(z+i)(z-i)} = \frac{1}{2i}[\frac{1}{z-i} - \frac{1}{z+i}]$](img912.png)
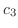
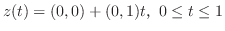 |
 |
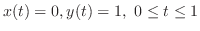 |
|
 |
![$\displaystyle \frac{1}{2i}[2\pi i - 2\pi i] = 0$](img916.png) |
曲線 は原点を中心とする半径1の円周であるので,
は原点を中心とする半径1の円周であるので,
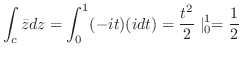 はこの円内で正則ではない.そこで,
はこの円内で正則ではない.そこで,
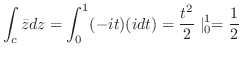 を部分分数分解すると
を部分分数分解すると
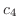
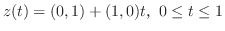
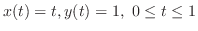 とおくと
とおくと
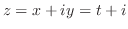
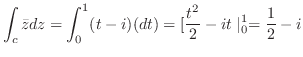 とくと
とくと
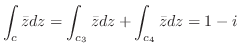
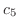 |
 |
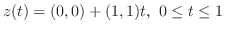 |
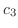
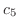 |
 |
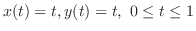 |
|
 |
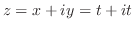 |
この曲線は原点を中心とし,半径 r > 1の円の上半円周と,実軸上の直径より,
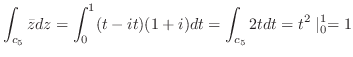 はこの曲線内で正則ではない.そこで,
はこの曲線内で正則ではない.そこで,
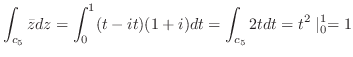 を部分分数分解する.
を部分分数分解する.
 の解は
の解は
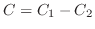
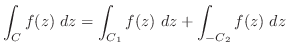
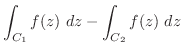
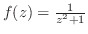 と
と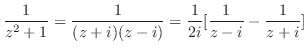 だけである.
だけである.
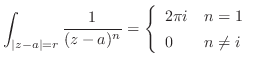 |
 |
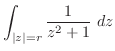 |
|
 |
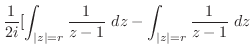 |
||
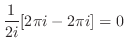 |
 |
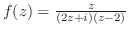 |
|
 |
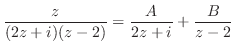 |
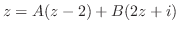 |
 |
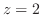 |
|
 |
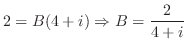 |
||
 |
![$\displaystyle \frac{\pi i}{2}[e^{\frac{-3\pi i}{4}} + e^{\frac{-9 \pi i}{4}}]$](img944.png) |
||
 |
![$\displaystyle \frac{\pi i}{2}[\frac{-1-i}{\sqrt{2}} + \frac{1-i}{\sqrt{2}}] = \frac{\pi}{2}$](img945.png) |
3.
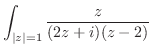
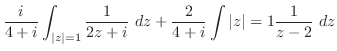
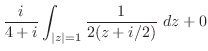
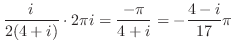 |
|||
 |
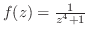 |
||
 |
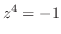 |
||
 |
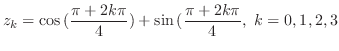 |
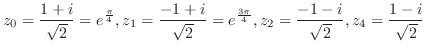
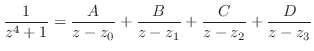
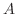 |
 |
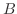 |
|
 |
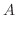 |
||
 |
![$\displaystyle \frac{1}{i}\log(-1 + \sqrt{2}) = \frac{1}{i}[\log_{e}\vert-1 + \sqrt{2}\vert + i\arg(-1 + \sqrt{2})]$](img958.png) |
||
 |
![$\displaystyle \frac{1}{i}[\log_{e}(\sqrt{2} - 1)]$](img959.png) |
4.
 を満たす関数
を満たす関数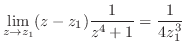 を調和関数という.また,
を調和関数という.また, をラプラシアンといい,
をラプラシアンといい,
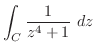 の式をラプラス方程式という.
の式をラプラス方程式という.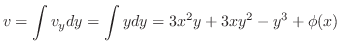 を実部にもつ正則関数
を実部にもつ正則関数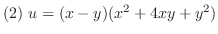 はコーシー・リーマンの方程式を満たすことを確認しておく.
はコーシー・リーマンの方程式を満たすことを確認しておく.
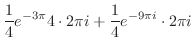
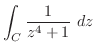 となるので,
となるので,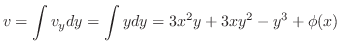 は調和関数.次に
は調和関数.次に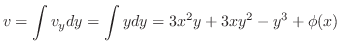 を実部にもつ正則関数
を実部にもつ正則関数 を求める.
を求める.
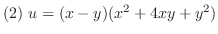 とおくと
とおくと
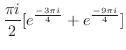
式A.1を
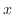 で偏微分すると
ここで,条件より
で偏微分すると
ここで,条件より
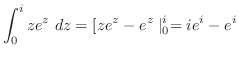 より
より
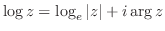 よって
よって
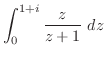 となり
となり
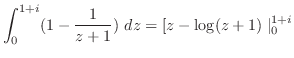
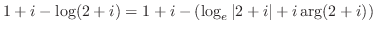
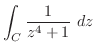 となるので,
となるので,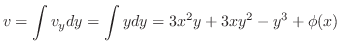 は調和関数.次に
は調和関数.次に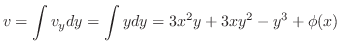 を実部にもつ正則関数
を実部にもつ正則関数 を求める.
を求める.
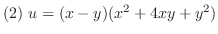 とおくと
とおくと
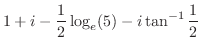
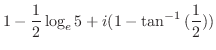 |
 |
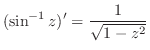 |
|
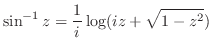 |
 |
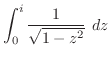 |
|
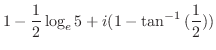 |
 |
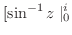 |
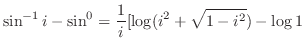
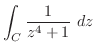 となるので,
となるので,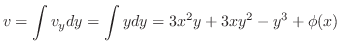 は調和関数.次に
は調和関数.次に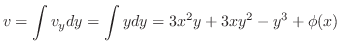 を実部にもつ正則関数
を実部にもつ正則関数 を求める.
を求める.
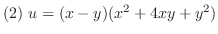 とおくと
とおくと
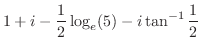
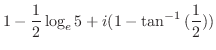 |
 |
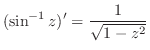 |
|
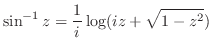 |
 |
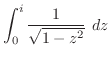 |
|
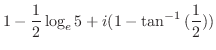 |
 |
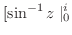 |
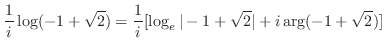
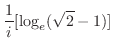
 となるので,
となるので,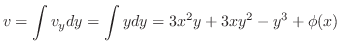 は調和関数.次に
は調和関数.次に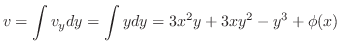 を実部にもつ正則関数
を実部にもつ正則関数 を求める.
を求める.
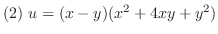 とおくと
とおくと
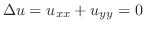
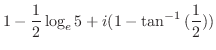 |
 |
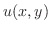 |
|
 |
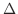 |
||
 |
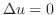 |
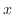 で偏微分すると
で偏微分すると
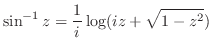 |
 |
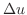 |
|
 |
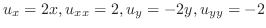 |
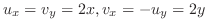 なので
なので
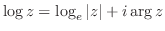 .よって
.よって
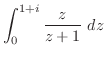 .これより
.これより