Next: 4.3 コーシーの積分定理 Up: 演習問題詳解 Previous: 4.1 線積分とグリーンの定理 索引
 |
 |
 |
|
 |
 |
||
 |
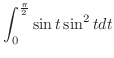 |
case1. 正方形の辺に沿って,積分経路を0から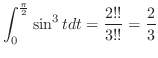 ,
,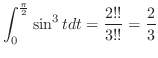 から
から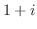 ととる.
ととる.
0と を結ぶ直線
を結ぶ直線 は,
は,
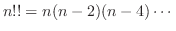 とパラメター化できる.したがって,
とパラメター化できる.したがって,
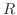 .
これより
.
これより
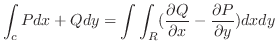 となり
となり
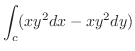
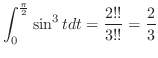 と
と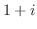 を結ぶ直線
を結ぶ直線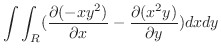 は,
は,
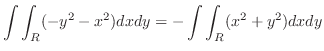 とパラメター化できる.したがって,
とパラメター化できる.したがって,
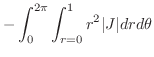 .
これより
.
これより
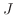 となり
となり
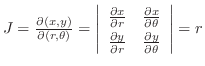
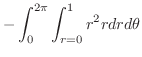
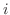 ,
,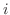 から
から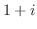 ととる.
ととる.
0と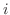 を結ぶ直線
を結ぶ直線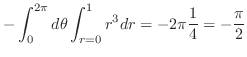 は,
は,
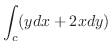 とパラメター化できる.したがって,
とパラメター化できる.したがって,
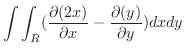 .
これより
.
これより
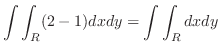 となり
となり
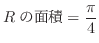
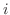 と
と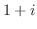 を結ぶ直線
を結ぶ直線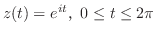 は,
は,
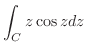 とパラメター化できる.したがって,
とパラメター化できる.したがって,
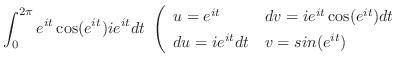 .
これより
.
これより
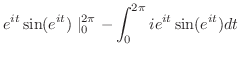 となり
となり
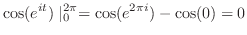
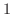
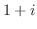 ととる.
ととる.
0と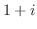 を結ぶ直線
を結ぶ直線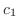 は,
は,
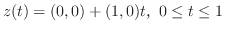 とパラメター化できる.したがって,
とパラメター化できる.したがって,
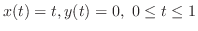 .
これより
.
これより
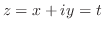 となり
となり