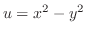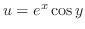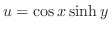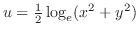Next: コーシーの積分表示(Cauchy's integral formula) Up: 複素積分 Previous: 複素積分(Complex integral) 索引
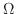 で関数
で関数 が正則であるとき,
が正則であるとき,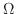 内の任意の単一閉曲線を
内の任意の単一閉曲線を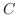 とし,
とし,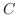 で囲まれた領域
で囲まれた領域
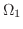 が
が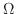 の内部にあるとすれば,常に
の内部にあるとすれば,常に
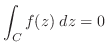
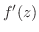 が連続の場合
が連続の場合
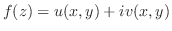 とおくと,
とおくと,
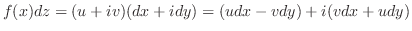 .
これより,
.
これより,
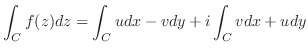
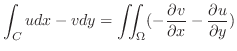
 は正則よりコーシー・リーマン(
は正則よりコーシー・リーマン(
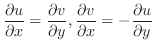 )の関係式が成り立つので,
)の関係式が成り立つので,
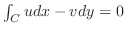 .
同様に,
.
同様に,
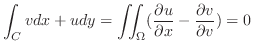
 が領域
が領域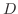 で正則であり,2点
で正則であり,2点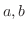 を結ぶ2つの曲線
を結ぶ2つの曲線
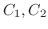 が
が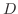 内にあり,かつ
内にあり,かつ
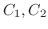 で囲まれた領域が
で囲まれた領域が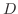 内にあれば,
内にあれば,
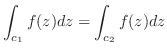
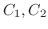 で囲まれた領域
で囲まれた領域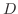 で
で が正則ならば,
が正則ならば,
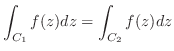
2. 次の関数を,示された閉曲線に沿って積分せよ.
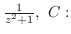 原点を中心とし,半径
原点を中心とし,半径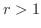 の円周
の円周
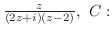 単位円
単位円
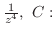 原点を中心とし,半径
原点を中心とし,半径 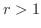 の円の上半円周と,実軸上の直径
の円の上半円周と,実軸上の直径
3. 次の積分を求めよ.積分路は下端と上端を結ぶ線分とする.
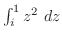
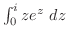
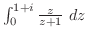
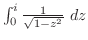
4. 次の関数が調和関数であることを証明し,それを実部にもつような正則関数を作れ.