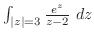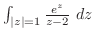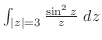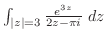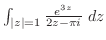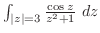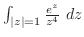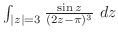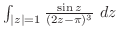Next: 展開と留数 Up: 複素積分 Previous: コーシーの積分定理(Cauchy's integral theorem) 索引
 が領域
が領域 で正則であるとする.
で正則であるとする. 内に単一閉曲線
内に単一閉曲線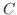 があり,
があり,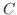 の内部も
の内部も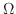 に含まれているとき,
に含まれているとき,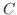 の内部の任意の点
の内部の任意の点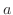 に対して次の公式が成り立つ.
に対して次の公式が成り立つ.
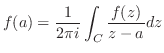
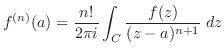
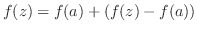 と書き直す.ここで,
と書き直す.ここで,
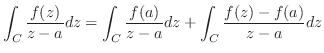
 の内部に点
の内部に点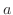 を含む半径
を含む半径
 の円を用意すると,
の円を用意すると,
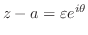 と表せる.これより,
と表せる.これより,
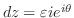 となり
となり
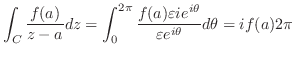
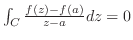 を示せばよい.
を示せばよい.
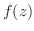 が連続より
が連続より
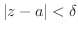 のとき
のとき
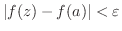 となる
となる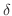 が存在する.そこで,点
が存在する.そこで,点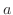 の周りの円
の周りの円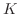 の半径
の半径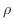 を
を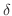 より小さくなるようにとると
より小さくなるようにとると
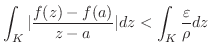
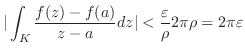
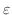 は限りなく小さくとれるので,
は限りなく小さくとれるので,
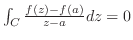
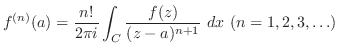
2. 次の積分を求めよ.