Next: 5.2 留数 Up: 演習問題詳解 Previous: 4.4 コーシーの積分表示 索引
1. 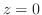 を中心としたローラン展開とは
を中心としたローラン展開とは
ローラン展開するには次のテーラー展開を知っていると便利である.
 |
 |
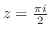 |
|
 |
 |
 |
|
 |
 |
 |
|
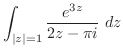 |
 |
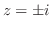 |
(a) 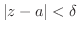 より
より
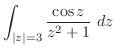 はテーラー展開できることに注意し,
はテーラー展開できることに注意し,
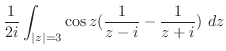 をまず,部分分数分解する.
をまず,部分分数分解する.
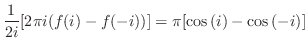 |
 |
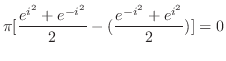 |
|
 |
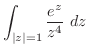 |
ここで
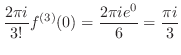 となるので
となるので
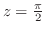
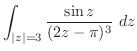 の分母を
の分母を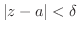 より2でくくると
より2でくくると
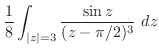
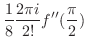 よりテーラー展開できるので
よりテーラー展開できるので
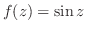 |
 |
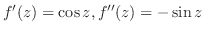 |
|
 |
 |
 |
 |
 |
|
 |
 |
||
 |
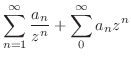 |
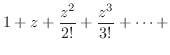
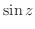 となりテーラー展開可能となることに注意し,
となりテーラー展開可能となることに注意し,
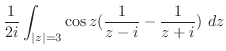 をまず,部分分数分解する.
をまず,部分分数分解する.
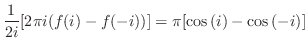 |
 |
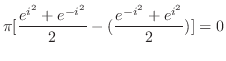 |
|
 |
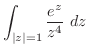 |
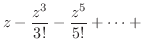 の分母を
の分母を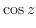 より
より でくくると
でくくると
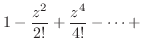 となるので
となるので
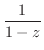 |
 |
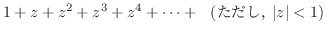 |
|
 |
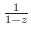 |
||
 |
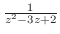 |
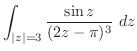 の分母を
の分母を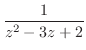 より2でくくると
より2でくくると
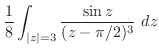
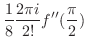 よりテーラー展開できるので
よりテーラー展開できるので
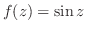 |
 |
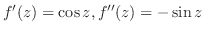 |
|
 |
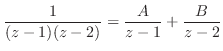 |
 |
 |
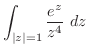 |
|
 |
 |
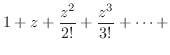
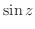 となりテーラー展開可能となることに注意し,
となりテーラー展開可能となることに注意し,
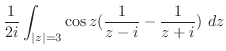 をまず,部分分数分解する.
をまず,部分分数分解する.
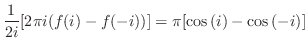 |
 |
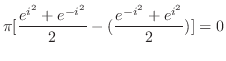 |
|
 |
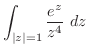 |
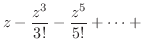 の分母を
の分母を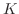 より
より でくくると
でくくると
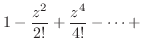 となるので
となるので
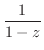 |
 |
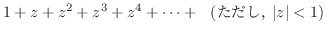 |
|
 |
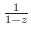 |
||
 |
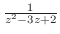 |
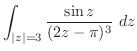 の分母を
の分母を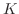 より
より でくくると
でくくると
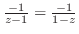
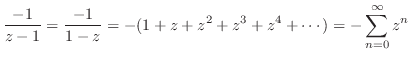 よりテーラー展開できるので
よりテーラー展開できるので
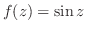 |
 |
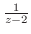 |
|
 |
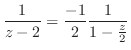 |
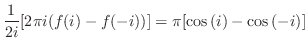 |
 |
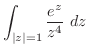 |
|
 |
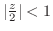 |
||
 |
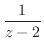 |
2.
(a) 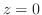 でのローラン展開なので
でのローラン展開なので
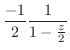 は何もする必要がない.したがって,
は何もする必要がない.したがって,
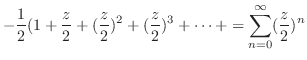 のテーラー展開を行なうと
のテーラー展開を行なうと
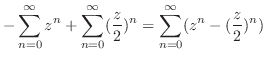
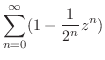 |
 |
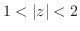 |
|
 |
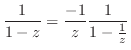 |
||
 |
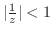 |
また,特異点0は3位の極
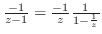
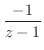 でのローラン展開となる.
でのローラン展開となる.
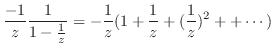 は何もする必要がない.したがって,
は何もする必要がない.したがって,
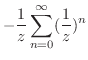 のテーラー展開を行なうと
のテーラー展開を行なうと
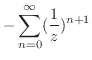
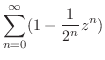 |
 |
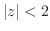 |
|
 |
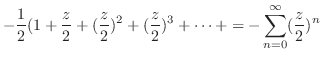 |
||
 |
![$\displaystyle -[\frac{1}{t} + 3 + 6t + 10t^2 + \cdots]$](img1078.png) |
||
 |
![$\displaystyle -[\frac{z+1} + 3 + 6(z+1) + 10(z+1)^2 + \cdots]$](img1079.png) |
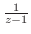 は1位の極
は1位の極
(c) 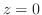 でのローラン展開なので
でのローラン展開なので
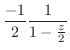 は何もする必要がない.したがって,
は何もする必要がない.したがって,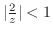 のテーラー展開を行なうと
のテーラー展開を行なうと
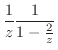
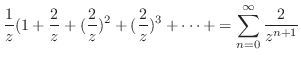 |
 |
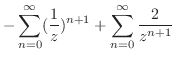 |
|
 |
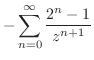 |
||
 |
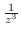 |
また,特異点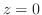 は3位の極
は3位の極
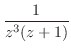
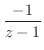 でのローラン展開となる.
でのローラン展開となる.
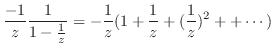 は何もする必要がない.したがって,
は何もする必要がない.したがって,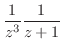 のテーラー展開を行なうと
のテーラー展開を行なうと
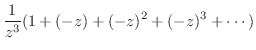
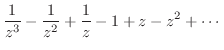 |
 |
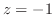 |
|
 |
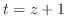 |
||
 |
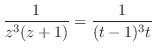 |
||
 |
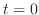 |
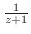 は除去可能な特異点
は除去可能な特異点