Next: 5.3 実積分への応用 Up: 演習問題詳解 Previous: 5.1 ローラン展開 索引
1. 特異点とは関数 が正則でない点のことである.有理関数では分母が0となる点のことである.
が正則でない点のことである.有理関数では分母が0となる点のことである.
基本公式
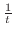
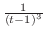 の積分は0にならないが,それ以外は全て0になる.このことから積分したときに0とならないものという意味で
の積分は0にならないが,それ以外は全て0になる.このことから積分したときに0とならないものという意味で
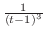 の係数を留数といい,
の係数を留数といい,![$Res[a]$](img452.png) と表わす.
と表わす.
留数公式
点 が
が の
の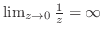 位の特異点のとき
位の特異点のとき
![$\displaystyle Res[a] = \frac{1}{(m-1)!}\lim_{z \to a}\frac{d^{m-1}}{dz^{m-1}}(z -a)^{m}f(z)$](img453.png)
(a) 分母が0となる点は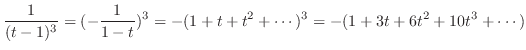 である.そこで
である.そこで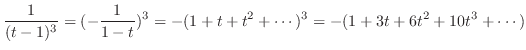 の留数を求める.
の留数を求める.
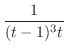 を部分分数分解すると
を部分分数分解すると
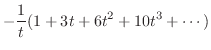
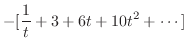
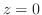 とおくと
とおくと
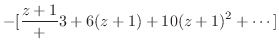
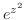 とおくと
とおくと
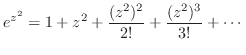
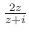 の係数合わせをすると
の係数合わせをすると
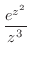
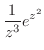
![$\displaystyle Res[0] = \frac{1}{z}の係数 = 1$](img1107.png)
![$\displaystyle Res[1] = \frac{1}{z-1}の係数 = -1$](img1108.png)
(b) 分母が0となる点は
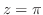 である.そこで
である.そこで
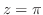 の留数を求める.
の留数を求める.
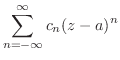 を部分分数分解すると
を部分分数分解すると
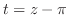
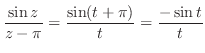
 とおくと
とおくと
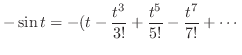 とおくと
とおくと
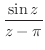
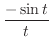
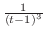 の係数であるので,次のように表わす.
の係数であるので,次のように表わす.
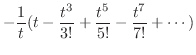
![$\displaystyle Res[2] = \frac{1}{z-2}の係数 = \frac{2}{5}$](img1117.png)
![$\displaystyle Res[-\frac{1}{2}] = \frac{1}{z+\frac{1}{2}}の係数 = \frac{1}{10}$](img1118.png)
(c) 分母が0となる点は
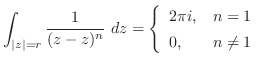 である.そこで
である.そこで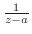 の留数を求める.
の留数を求める.
 は部分分数分解できないので,
は部分分数分解できないので,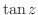 を
を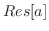 でテーラー展開し,その後割り算をする.そこで
でテーラー展開し,その後割り算をする.そこで
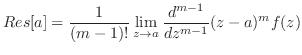 とおくと
とおくと
 が偶数の場合を考えると
が偶数の場合を考えると
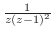 |
 |
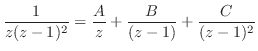 |
|
 |
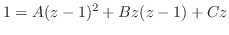 |
||
 |
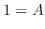 |
![$\displaystyle Res[n\pi] = \frac{1}{z-n\pi}の係数 = 1$](img1128.png)
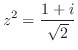 が奇数の場合を考えると
が奇数の場合を考えると
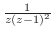 |
 |
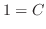 |
|
 |
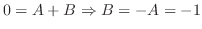 |
||
 |
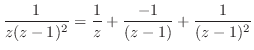 |
![$\displaystyle Res[n\pi] = \frac{1}{z-n\pi}の係数 = -1$](img1132.png)
(d) 分母が0となる点は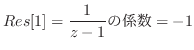 である.そこで
である.そこで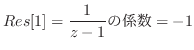 の留数を求める.
の留数を求める.
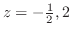 を部分分数分解すると
を部分分数分解すると
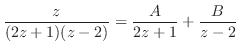
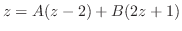
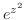 とおくと
とおくと
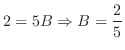
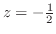 とおくと
とおくと
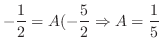
![$\displaystyle Res[1] = \frac{1}{z-1}の係数 = \frac{e}{9}$](img1140.png)
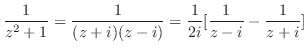 を求めたいのだが,係数合わせは使えない.なぜなら
を求めたいのだが,係数合わせは使えない.なぜなら は多項式ではない.そこで,へービサイドの展開定理を用いるか留数公式を用いる.ここでは留数公式を用いる.
は多項式ではない.そこで,へービサイドの展開定理を用いるか留数公式を用いる.ここでは留数公式を用いる.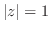 は2位の極なので
は2位の極なので
![$\displaystyle Res[-2] = \frac{1}{(2-1)!}\lim_{z \to -2}\frac{d}{dz}(z +2)^{2} \frac{e^z}{(z-1)(z+2)^2} = -\frac{4e^{-2}}{9} $](img1141.png)
2. 留数定理
関数 が単一閉曲線
が単一閉曲線 の上および内部で,その内部にある有限個の点
の上および内部で,その内部にある有限個の点
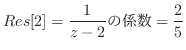 を除いて正則な1価関数であるとき
を除いて正則な1価関数であるとき
![$\displaystyle \int_{C}f(z) dz = 2\pi i\{Res[a_{1}] + Res[a_{2}] + \cdots + Res[a_{n}]\}$](img1143.png)
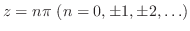 |
 |
![$\displaystyle 2\pi i\{Res[0] + Res[1]\} (z=0,1は\vert z\vert = 2に含まれる)$](img1145.png) |
|
 |
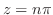 |
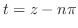 |
 |
![$\displaystyle 2\pi i Res[-\frac{1}{2}] (z=2は\vert z\vert = 1に含まれない)$](img1148.png) |
|
 |
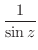 |
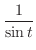 |
 |
![$\displaystyle 2\pi i Res[0] (z=0だけ\vert z\vert = 1に含まれる)$](img1151.png) |
|
 |
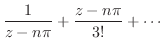 |
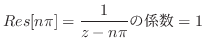 |
 |
![$\displaystyle 2\pi i (Res[1] + Res[-2]) (z=1,2は\vert z\vert = 3に含まれる)$](img1154.png) |
|
 |
 |
||
 |
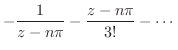 |
3.
![$\displaystyle Res[0]$](img1158.png) |
 |
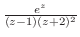 |
|
 |
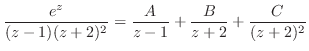 |
||
 |
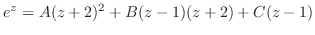 |
||
 |
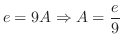 |
![$\displaystyle \int_{\vert z\vert=1}\frac{e^{2z}}{z^{2}(z^2 + 2z + 2)} dz = 2\pi i Res[0] = \pi i$](img1163.png)
(b) 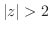 の円には特異点
の円には特異点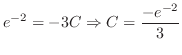 が含まれる.ここで
が含まれる.ここで![$Res[0]$](img1157.png) はすでにA.14で求めたので
はすでにA.14で求めたので![$Res[-1+i]$](img1165.png) を求めると
を求めると
![$\displaystyle Res[-1+i]$](img1166.png) |
 |
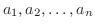 |
|
 |
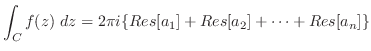 |
||
 |
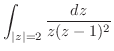 |
||
 |
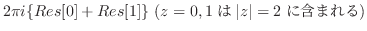 |
よって留数定理より
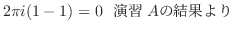 |
 |
![$\displaystyle 2\pi i (Res[0] + Res[-1+i])$](img1172.png) |
|
 |
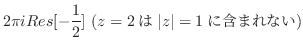 |
(c) 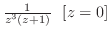 の円には特異点
の円には特異点
 の全てが含まれる.ここで
の全てが含まれる.ここで
![$Res[0], Res[-1+i]$](img1175.png) はすでにA.14で求めたので
はすでにA.14で求めたので![$Res[-1-i]$](img1176.png) を求めると
を求めると
![$\displaystyle Res[-1-i]$](img1177.png) |
 |
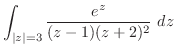 |
|
 |
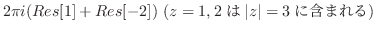 |
||
 |
 |
||
 |
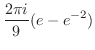 |
よって留数定理より
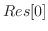 |
 |
![$\displaystyle 2\pi i (Res[0] + Res[-1+i] + Res[-1-i])$](img1183.png) |
|
 |
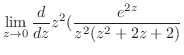 |
||
 |
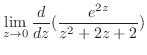 |
||
 |
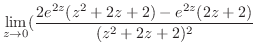 |
||
 |
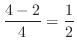 |