Next: 関数の極限(limit of function) Up: 関数(FUNCTIONS) Previous: 関数の定義(definition of function) 索引
|
 軸とのなす角を求めよう.ただし,
軸とのなす角を求めよう.ただし,
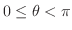 .
.
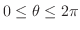 とします.
とします.
|
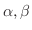 に対して,次の公式が成り立つことを示そう.
に対して,次の公式が成り立つことを示そう.
(a)
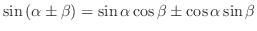 (加法定理)
(加法定理)
(b)
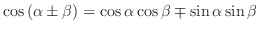 (複号同順)
(複号同順)
(c)
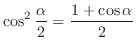 (半角の公式)
(半角の公式)
(d)
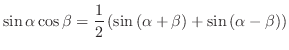 (積から和への公式)
(積から和への公式)
(e)
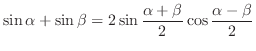 (和から積への公式)
(和から積への公式)
 において,
において,
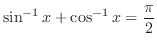 が成り立つことを示そう.
が成り立つことを示そう.