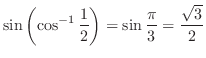Next: 1.3 関数の極限 Up: 確認問題詳解 Previous: 1.1 関数 索引
1.
2.
(a) 直線と 軸とのなす角は,直線の傾きより求める.
軸とのなす角は,直線の傾きより求める.
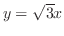 の傾きは
の傾きは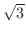 .つまり,
.つまり, 軸方向に1変化すると
軸方向に1変化すると 軸方向に
軸方向に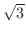 変化する.これより,1:2:
変化する.これより,1:2: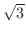 の直角三角形を思い起こすと,
の直角三角形を思い起こすと, 軸と直線のなす角は
軸と直線のなす角は
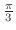 となる.
となる.
(b) 直線と 軸とのなす角は,直線の傾きより求める.
軸とのなす角は,直線の傾きより求める.
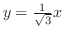 の傾きは
の傾きは
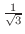 .つまり,
.つまり, 軸方向に
軸方向に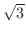 変化すると
変化すると 軸方向に
軸方向に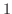 変化する.これより,1:2:
変化する.これより,1:2: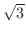 の直角三角形を思い起こすと,
の直角三角形を思い起こすと, 軸と直線のなす角は
軸と直線のなす角は
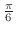 となる.
となる.
3.
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren1-2-3a.eps}
\end{figure}](img1219.png)
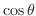 が
が
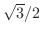 より大きい
より大きい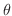 の範囲を求めたいので,単位円を描き,
の範囲を求めたいので,単位円を描き, の値が
の値が
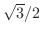 より大きくなる範囲を求めればよい.そこで,
より大きくなる範囲を求めればよい.そこで, 軸上に
軸上に
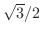 の点をとり,
の点をとり, 軸に平行にこの点を通るように直線を引く.この直線と単位円の交点に原点から直線を引く.これで,
軸に平行にこの点を通るように直線を引く.この直線と単位円の交点に原点から直線を引く.これで,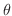 の範囲は
の範囲は
![$[0,\frac{\pi}{6}) \cup (\frac{11\pi}{6},2\pi]$](img1223.png) となる.
となる.
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren1-2-3b.eps}
\end{figure}](img1224.png)
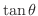 が
が
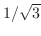 より大きい
より大きい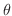 の範囲を求めたいので,単位円を描き,傾き
の範囲を求めたいので,単位円を描き,傾き
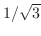 の直線を引く.この直線と単位円の交点から
の直線を引く.この直線と単位円の交点から 軸までの間,
軸までの間,
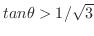 を満たす.したがって,
を満たす.したがって,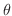 の範囲は
の範囲は
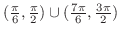 となる.
となる.
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren1-2-3c.eps}
\end{figure}](img1229.png)
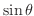 が
が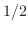 より大きい
より大きい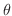 の範囲と
の範囲と
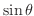 が
が
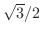 より小さい範囲の積集合を求めればよい.そこで,
より小さい範囲の積集合を求めればよい.そこで, 軸上に
軸上に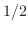 と
と
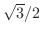 の点をとり,
の点をとり, 軸に平行にこれらの点を通るように直線を引く.これらの直線と単位円の交点に原点から直線を引く.これで,
軸に平行にこれらの点を通るように直線を引く.これらの直線と単位円の交点に原点から直線を引く.これで,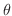 の範囲は
の範囲は
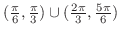 となる.
となる.
4.
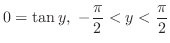
 は0しかないので、
は0しかないので、
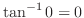
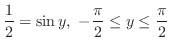
 は
は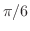 しかないので、
しかないので、
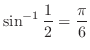
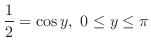
 は
は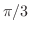 しかないので、
しかないので、
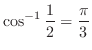 . これより、
. これより、