Next: 1.2 初等関数 Up: 確認問題詳解 Previous: 0.2 不等式(INEQUALITIES) 索引
1.
2.
(a) すべての実数 に対して
に対して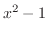 は実数となる.したがって,
は実数となる.したがって,
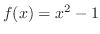 の定義域は
の定義域は
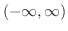 .
.
すべての に対して,
に対して,
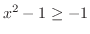 が成り立つ.したがって,
が成り立つ.したがって,
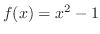 の値域は
の値域は
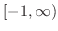 .
.
(b)
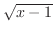 は
は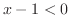 のとき定義されない.したがって,
のとき定義されない.したがって,
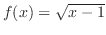 の定義域は
の定義域は
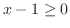 .つまり,
.つまり,
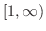 .
.
定義域内のすべての に対して,
に対して,
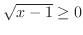 が成り立つ.したがって,
が成り立つ.したがって,
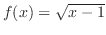 の値域は
の値域は
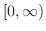 .
.
(c) すべての実数 に対して
に対して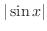 は実数となる.したがって,
は実数となる.したがって,
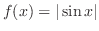 の定義域は
の定義域は
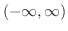 .
.
すべての に対して,
に対して,
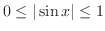 が成り立つ.したがって,
が成り立つ.したがって,
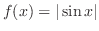 の値域は
の値域は![$[0,1]$](img146.png) .
.
3.
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren1-1-3a.eps}
\includegraphics[width=5cm]{CALCFIG/ren1-1-3b.eps}
\end{figure}](img1158.png)
4.
また,
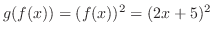
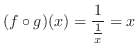
また,
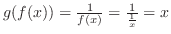
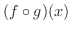 |
 |
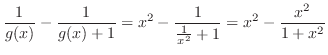 |
|
 |
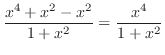 |
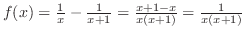 より,
より,
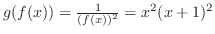
5.
(a)
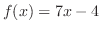 は1対1の関数であることを示す.つまり,
は1対1の関数であることを示す.つまり,
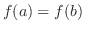 ならば,
ならば,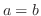 を示せばよい.
を示せばよい.
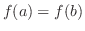 |
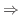 |
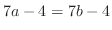 |
|
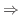 |
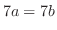 |
||
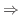 |
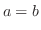 |
したがって,
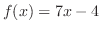 にはただ1つの逆関数が存在する.
にはただ1つの逆関数が存在する.
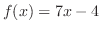 の逆関数
の逆関数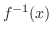 は
は
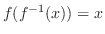 を満たす.したがって,
を満たす.したがって,
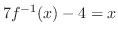 より,
より,
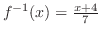
(b)
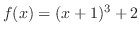 は1対1の関数であることを示す.つまり,
は1対1の関数であることを示す.つまり,
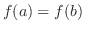 ならば,
ならば,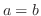 を示せばよい.
を示せばよい.
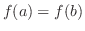 |
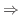 |
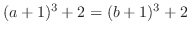 |
|
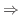 |
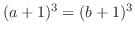 |
||
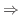 |
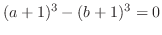 |
||
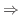 |
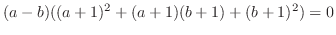 |
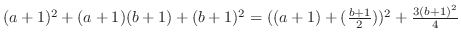 より,どんな実数
より,どんな実数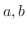 でも0にならない.したがって,
でも0にならない.したがって,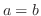 が成り立つ.
が成り立つ.
次に,
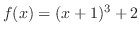 の逆関数
の逆関数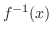 を求める.
を求める.
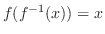 より
より
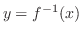 とおくと,
とおくと,
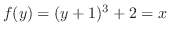 となる.この式を
となる.この式を について求めればよい.
について求めればよい.
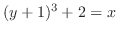 |
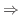 |
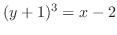 |
|
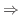 |
![$\displaystyle y+1 = \sqrt[3]{x-2}$](img1200.png) |
||
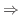 |
![$\displaystyle y = \sqrt[3]{x-2} - 1$](img1201.png) |
(c)
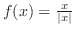 は2つの異なる値
は2つの異なる値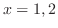 に対して,
に対して,
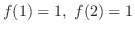 となるので,1対1の関数ではない.
となるので,1対1の関数ではない.
6.