Next: 初等関数(elementary functions) Up: 関数(FUNCTIONS) Previous: 関数(FUNCTIONS) 索引
|
 の値が1のとき
の値が1のとき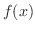 の値を求めよう.
の値を求めよう.
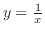 および
および
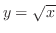 のグラフをもとに次の関数のグラフの概形を描こう.
のグラフをもとに次の関数のグラフの概形を描こう.
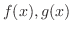 について,
について,
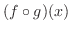 と
と 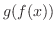 を求めよう.
を求めよう.
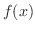 は,
は,
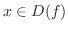 で,
で,
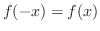 を満たすとき偶関数(even function)であるといい,
を満たすとき偶関数(even function)であるといい,
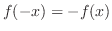 を満たすとき奇関数(odd function)であるといいます.次の関数は偶関数か奇関数か調べよう.
を満たすとき奇関数(odd function)であるといいます.次の関数は偶関数か奇関数か調べよう.
|
 価関数か多価関数か調べよう.
価関数か多価関数か調べよう.
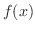 のグラフを描こう.
のグラフを描こう.
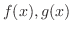 について,
について,
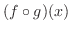 と
と 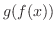 を求めよう.
を求めよう.
(a) 偶関数と偶関数の積と偶関数と奇関数の積はどうなるか.
(b) 偶関数の特徴と奇関数の特徴について述べよう.