Next: 合成関数の偏微分法(differentiation of composite functions Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: 全微分(total differential) 索引
|
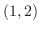 で
で 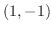 の方向に微分しよう.
の方向に微分しよう.
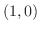 で
で
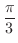 方向に微分しよう.
方向に微分しよう.
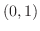 で
で 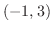 方向に微分しよう.また方向微分が最大になるような方向単位ベクトルを求めよう.
方向に微分しよう.また方向微分が最大になるような方向単位ベクトルを求めよう.
|
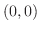 で
で
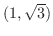 の方向に微分しよう.
の方向に微分しよう.
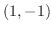 で
で
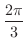 方向に微分しよう.
方向に微分しよう.
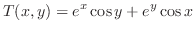
(a) 点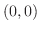 からどの方向に進むと,温度上昇が最も大きいか.また,そのときの温度の変化率を調べよう.
からどの方向に進むと,温度上昇が最も大きいか.また,そのときの温度の変化率を調べよう.
(b) 点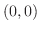 からどの方向に進むと,温度下降が最も大きいか.また,そのときの温度の変化率を調べよう.
からどの方向に進むと,温度下降が最も大きいか.また,そのときの温度の変化率を調べよう.