Next: 6.6 合成関数の偏微分法 Up: 確認問題詳解 Previous: 6.4 全微分 索引
1.
方向微分は
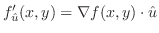
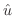 は
は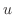 方向の単位ベクトルを表わす.
方向の単位ベクトルを表わす.
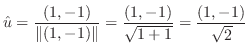
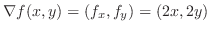
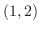 における方向微分は
における方向微分は
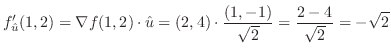
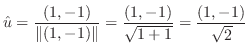
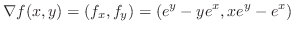
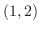 における方向微分は
における方向微分は
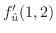 |
 |
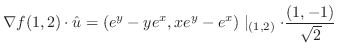 |
|
 |
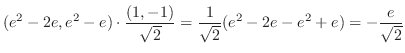 |
2.
(a)
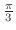 方向とは,
方向とは, 軸から
軸から
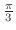 の方向のことである.そこで,単位方向ベクトル
の方向のことである.そこで,単位方向ベクトル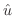 を求めると
を求めると
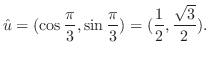
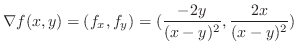
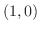 における方向微分は
における方向微分は
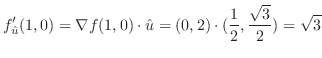
(b)
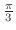 方向とは,
方向とは, 軸から
軸から
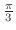 の方向のことである.そこで,単位方向ベクトル
の方向のことである.そこで,単位方向ベクトル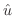 を求めると
を求めると
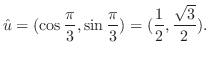
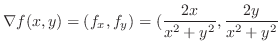
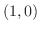 における方向微分は
における方向微分は
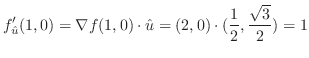
3.
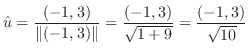
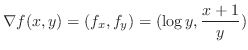
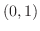 における方向微分は
における方向微分は
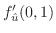 |
 |
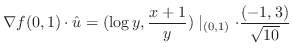 |
|
 |
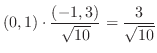 |
次に方向微分が最大になる方向単位ベクトルは,
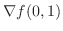 と同じ方向であるから,
と同じ方向であるから,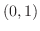 となる.
となる.
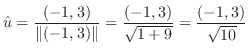
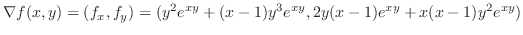
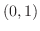 における方向微分は
における方向微分は
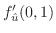 |
 |
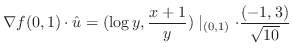 |
|
 |
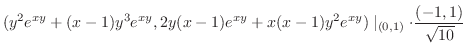 |
||
 |
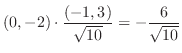 |
次に方向微分が最大になる方向単位ベクトルは,
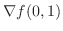 と同じ方向であるから,
と同じ方向であるから,
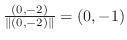 となる.
となる.