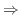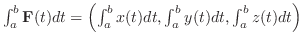Next: 曲線(space curves) Up: ベクトル関数(VECTOR FUNCTIONS) Previous: ベクトル関数(VECTOR FUNCTIONS) 索引
|
|
(a)
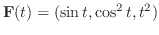 のとき,
のとき,
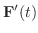 を求めよう.
を求めよう.
(b)
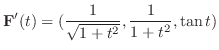 のとき,
のとき,
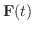 を求めよう.
を求めよう.
(c)
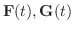 が
が  について微分可能なベクトル関数のとき,
について微分可能なベクトル関数のとき,
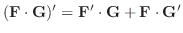
(d)
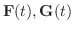 が
が  について微分可能なベクトル関数のとき,
について微分可能なベクトル関数のとき,
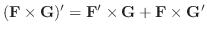
(e)
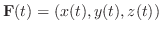 とすると,次のことが成り立つことを示そう.
(b)
とすると,次のことが成り立つことを示そう.
(b)
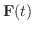 は連続
は連続
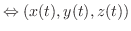 が共に連続よう.
が共に連続よう.
(c)
![${\bf F} \in C'[a,b] \Rightarrow {\bf F}'(t_{0}) = (x'(t_{0}),y'(t_{0}),z'(t_{0}))$](img640.png)
(d)
![${\bf F} \in C[a,b]$](img641.png)