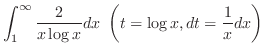Next: 6. 偏微分法(PARTIAL DIFFERENTIATION) Up: 演習問題詳解 Previous: 5.2 解答 索引
5.3
1.
1.
位置ベクトル
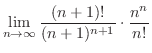 に対して,
に対して,
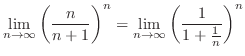 は速度ベクトルを意味する.幾何学的には運動している物体の接線方向のベクトルである.また,
は速度ベクトルを意味する.幾何学的には運動している物体の接線方向のベクトルである.また,
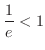 は加速度ベクトルで,幾何学的には,接線方向の加速度ベクトル
は加速度ベクトルで,幾何学的には,接線方向の加速度ベクトル
 と法線方向の加速度ベクトル
と法線方向の加速度ベクトル
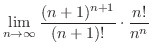 の和で表わされる.つまり
の和で表わされる.つまり
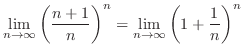
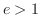 は接線単位ベクトル,
は接線単位ベクトル,
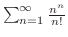 は法線単位ベクトルを表わす.
言い換えると,
は法線単位ベクトルを表わす.
言い換えると,
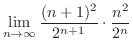
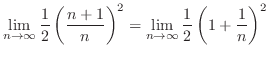
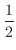
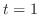 のとき
のとき
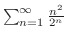
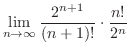
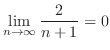
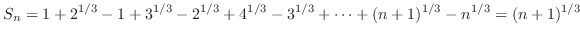
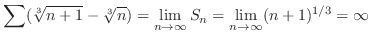
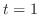 のとき
のとき
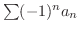
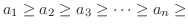
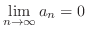
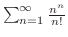 を求める.
を求める.
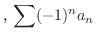 |
 |
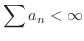 |
|
 |
 |
 |
 |
 |
|
 |
 |
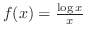 とおくと,
とおくと,
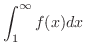 より
より
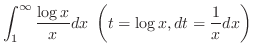
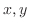 について解くと
について解くと
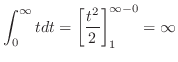
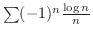
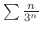
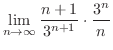
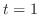 のとき
のとき
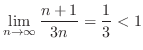
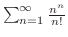 を求める.
を求める.
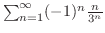 |
 |
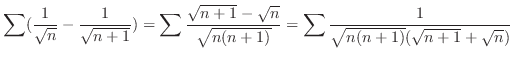 |
|
 |
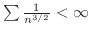 |
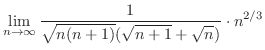 |
 |
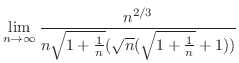 |
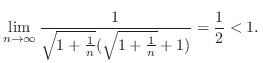
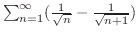
2.