Next: 定積分の定義の拡張(extension of definite integrals) Up: 積分法(INTEGRATION) Previous: 定積分(definite integral) 索引
|
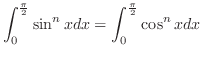 を示そう.
を示そう.
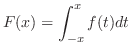 について以下のことについて答えよう.ただし,
について以下のことについて答えよう.ただし,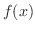 は区間
は区間
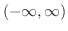 で微分可能な関数とする.
で微分可能な関数とする.
(a) 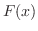 は奇関数であることを示そう.
は奇関数であることを示そう.
(b) 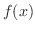 が偶関数ならば
が偶関数ならば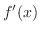 は奇関数であることを示そう.
は奇関数であることを示そう.
(c)
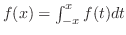 ならば
ならば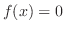 となることを示そう.
となることを示そう.
(d) 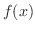 は偶関数と奇関数の和で表せることを示そう.
は偶関数と奇関数の和で表せることを示そう.