Next: 4. 級数(SERIES) Up: 演習問題詳解 Previous: 3.9 解答 索引
3.10
1.
図形の面積を求めるには図を描く.
(a)
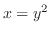 と
と
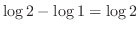 の交点を求めると
の交点を求めると
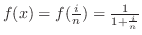 より
より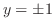 となる.つまり,この2つの曲線は点
となる.つまり,この2つの曲線は点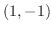 と点
と点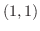 で交わっている.そこでこの図形の面積は横方向の長方形の面積
で交わっている.そこでこの図形の面積は横方向の長方形の面積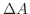 の和として考える.
の和として考える. 軸に垂直な直線でこの図形を切断するとその幅は,右側の曲線 - 左側の曲線で与えられ,また高さは
軸に垂直な直線でこの図形を切断するとその幅は,右側の曲線 - 左側の曲線で与えられ,また高さは 軸方向に小さな幅となるので
軸方向に小さな幅となるので 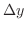 で与えられる.よって
で与えられる.よって
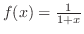
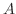 は
は
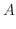 |
 |
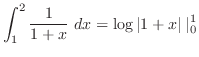 |
|
 |
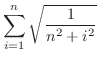 |
この図形は
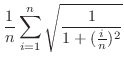 で微分可能ではないので,面積を求めるには
で微分可能ではないので,面積を求めるには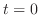 から
から
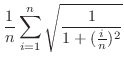 までの面積を求めて2倍する.縦方向に小さな幅を持つ長方形で切断すると切断面の面積
までの面積を求めて2倍する.縦方向に小さな幅を持つ長方形で切断すると切断面の面積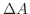 は
は
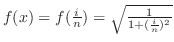
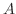 は
は
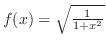
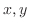 は
は でパラメター化されていることに注意すると,
でパラメター化されていることに注意すると,
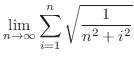
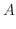 |
 |
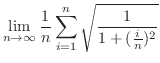 |
|
 |
 |
||
 |
 |
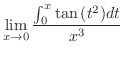
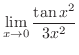 を表わす.
これより,
を表わす.
これより,
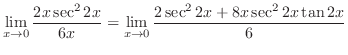
2.
(a)
回転軸に垂直な平面で切断すると,その断面はワッシャーと呼ばれる5円玉のような形になる.その断面積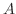 は全体の面積から中の面積を引いたものになる.
は全体の面積から中の面積を引いたものになる.
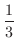 より
より
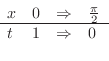 .これより
.これより
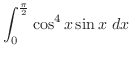
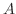 は
は
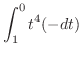
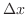 をつけると,その体積
をつけると,その体積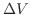 は
は
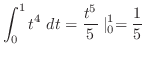
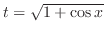
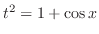 とおくと,
とおくと,
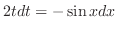 ,
,
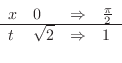 となるので,
となるので,
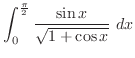
(b)
この関数の図形はサイクロイドと呼ばれる. 軸との交点は
軸との交点は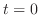 と
と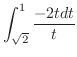 のときである.この図形を
のときである.この図形を 軸に回転してできる回転体を
軸に回転してできる回転体を 軸に垂直な平面で切断すると,その断面積は
軸に垂直な平面で切断すると,その断面積は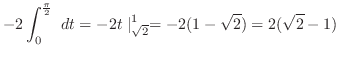 となる.これに少しの厚み
となる.これに少しの厚み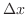 を付けると,その体積は
を付けると,その体積は
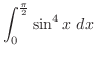
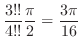
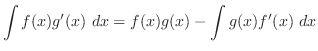 で対称となるので
で対称となるので
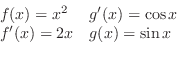
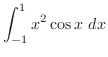 をパラメター
をパラメター で表わすと
で表わすと
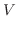 |
 |
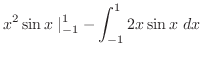 |
|
 |
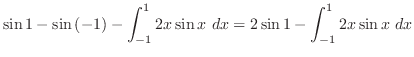 |
||
 |
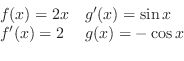 |
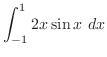 であることを用いると
であることを用いると
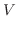 |
 |
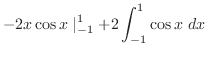 |
|
 |
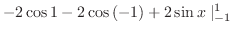 |
||
 |
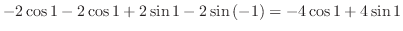 |
3.
(a)
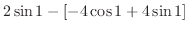 のグラフはアステロイドと呼ばれる.これをパラメター化すると
のグラフはアステロイドと呼ばれる.これをパラメター化すると
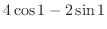 となる.
ここで,
となる.
ここで,
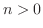 の長さを求めて4倍する.曲線の1部分
の長さを求めて4倍する.曲線の1部分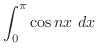 は
は
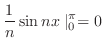
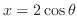 |
 |
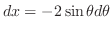 |
|
 |
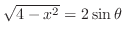 |
||
 |
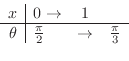 |
||
 |
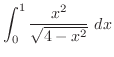 |
||
 |
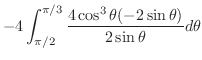 |
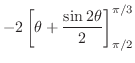
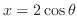 |
 |
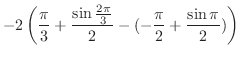 |
|
 |
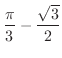 |
||
 |
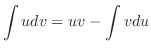 |
||
 |
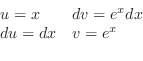 |
||
 |
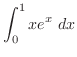 |
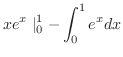 とおくと
とおくと
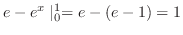 .また
.また
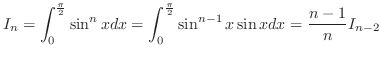
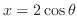 |
 |
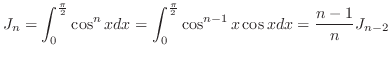 |
|
 |
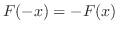 |
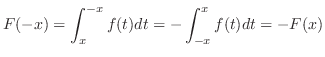 とおくと
とおくと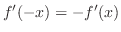
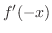
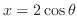 |
 |
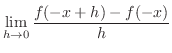 |
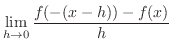
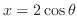 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
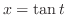
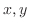 を極形式になおすと,
を極形式になおすと,
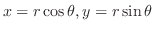 .よって
.よって
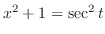 |
 |
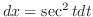 |
|
 |
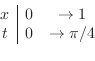 |
||
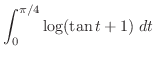 |
 |
 |
|
 |
 |
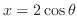 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
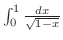 |
||
 |
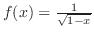 |
||
 |
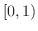 |
||
 |
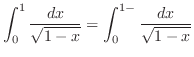 |