Next: 3.10 解答 Up: 演習問題詳解 Previous: 3.8 解答 索引
3.9
1.
広義積分を行なう前に次のような記号を理解する.
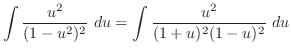
(a)
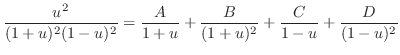 の積分を行なう前に,
の積分を行なう前に,
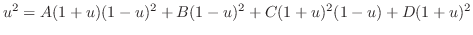 は
は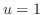 で連続であることに注意すると
で連続であることに注意すると
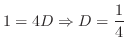
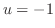 とおくと
とおくと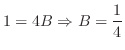 より
より
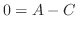 .また,
.また,
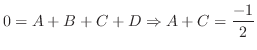
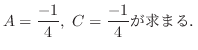 |
 |
 |
|
 |
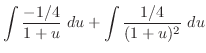 は0にならない は0にならない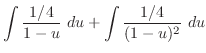 |
||
 |
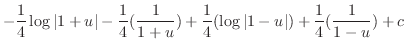 |
(b)
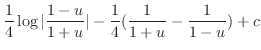 の積分を行なう前に,
の積分を行なう前に,
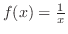 は
は![$(0,1]$](img3907.png) で連続であることに注意すると
で連続であることに注意すると
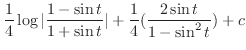
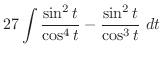 |
 |
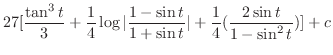 |
(c)
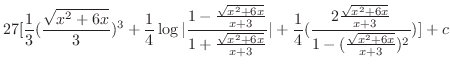 の積分を行なう前に,
の積分を行なう前に,
 は
は![$(0,1]$](img3907.png) で連続であることに注意すると
で連続であることに注意すると
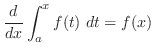
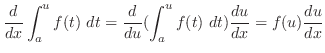
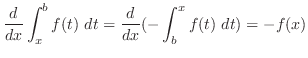 |
 |
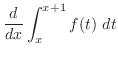 |
|
 |
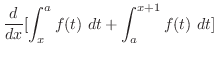 |
||
 |
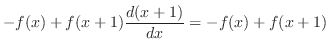 |
||
 |
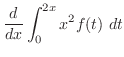 |
||
 |
 ロピタルの定理より ロピタルの定理より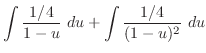 |
||
 |
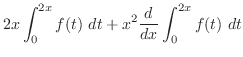 |
2.
(a)
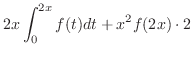 の積分を行なう前に,
の積分を行なう前に,
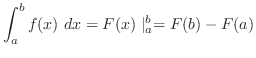 は
は
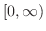 で連続であることに注意すると
で連続であることに注意すると
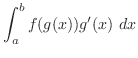
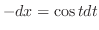
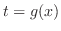
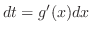 |
 |
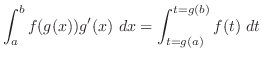 |
|
 |
 |
||
 |
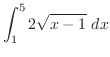 |
||
 |
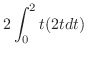 ロピタルの定理 ロピタルの定理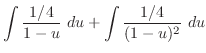 |
(b)
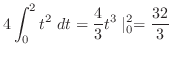 の積分を行なう前に,
の積分を行なう前に,
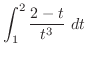 は
は
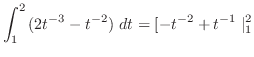 で連続であることに注意すると
で連続であることに注意すると
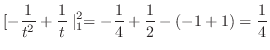
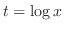 とおくと
とおくと
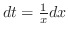 .このとき積分範囲は
.このとき積分範囲は
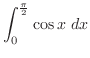
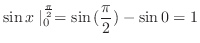 |
 |
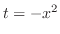 |
|
 |
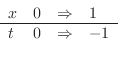 |
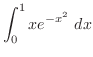
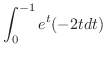
(c)
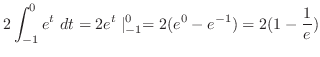 の積分を行なう前に,
の積分を行なう前に,
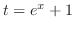 は
は
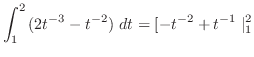 で連続であることに注意すると
で連続であることに注意すると
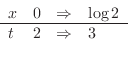
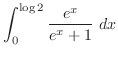
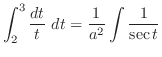
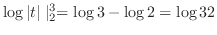 は
は
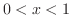 で収束.
次に,
で収束.
次に,
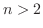 のとき,
のとき,
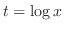 とおくと
とおくと
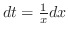 .また,
.また,
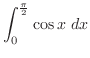
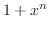 |
 |
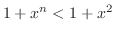 |
|
 |
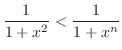 |
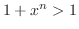 で
で
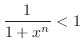 のとき
のとき
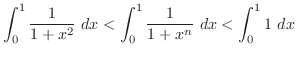 より
より
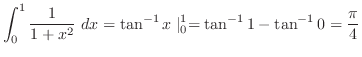
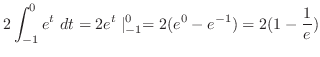 は発散.
は発散.
3.
(a) この問題は収束,発散について調べろという問題であり,何に収束するかという問題ではない.まず,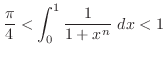 のテーラー展開を思いだすと
のテーラー展開を思いだすと
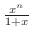
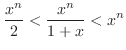
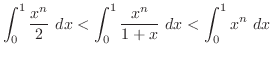
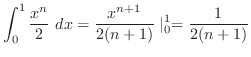 は上からの押さえることができた.ここで,
は上からの押さえることができた.ここで,
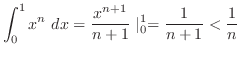
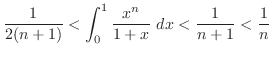 |
 |
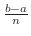 |
|
 |
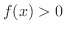 |
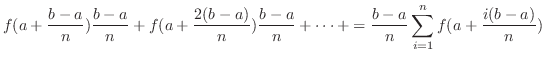
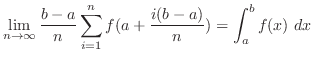 |
 |
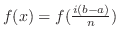 |
|
 |
![$\displaystyle 4[t\log{t} - t\mid_{0+}^{1} = 4[\log{1} - 1 - \lim_{t \to 0+}(t\log{t} - t)]$](img3968.png) |
||
 |
![$\displaystyle 4[-1 - \lim_{t \to 0+}(\frac{\log{t} -1}{\frac{1}{t}})]$](img3969.png) |
||
 |
![$\displaystyle 4[-1 - \lim_{t \to 0+}\frac{1/t}{-1/t^2} ] = -4$](img3970.png) |