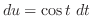Next: 3.9 解答 Up: 演習問題詳解 Previous: 3.7 解答 索引
3.8
1.
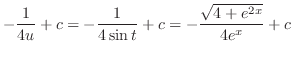
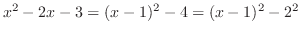 |
 |
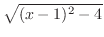 |
|
 |
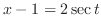 |
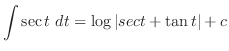
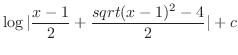 |
 |
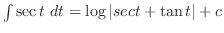 |
|
 |
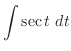 |
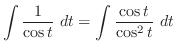 |
 |
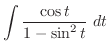 |
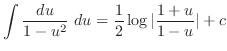
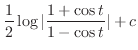
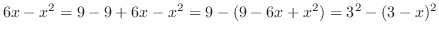 |
 |
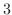 |
|
 |
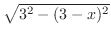 |
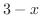
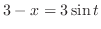 |
 |
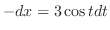 |
|
 |
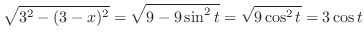 |
||
 |
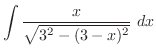 |
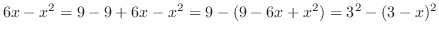 |
 |
![$\displaystyle 2\sin{1} -[-4\cos{1} + 4\sin{1}]$](img3847.png) |
|
 |
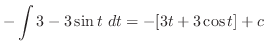 |
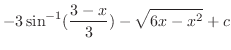 |
 |
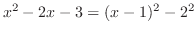 |
 |
 |
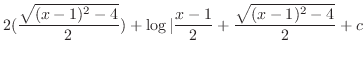 |
|
 |
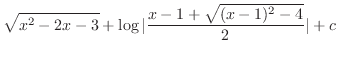 |
||
 |
![$\displaystyle -2\left[\theta + \frac{\sin{2\theta}}{2}\right]_{\pi/2}^{\pi/3}$](img3859.png) |
||
 |
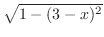 |
||
 |
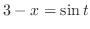 |
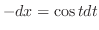
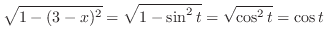
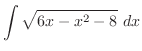 |
 |
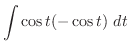 |
|
 |
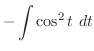 |
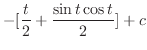
3.
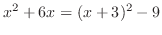
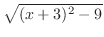 |
 |
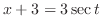 |
|
 |
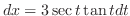 |
||
 |
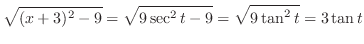 |
(d)
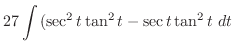 とおくと,
とおくと,
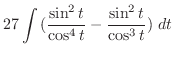 は偶関数.
は偶関数.
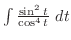 は奇関数となる.なぜならば,
は奇関数となる.なぜならば,
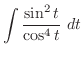
4.
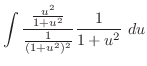 とおくと,
とおくと,
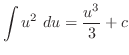 ,
,
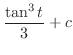 ,
,
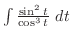 . よって,
. よって,
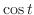
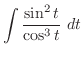 とおくと,
とおくと,
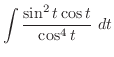 より,
より,
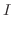 |
 |
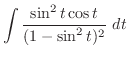 |
|
 |
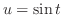 |