Next: 定積分の計算(calculation of integrals) Up: 積分法(INTEGRATION) Previous: 無理関数の積分法(integration of irrational functions) 索引
|
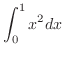 を求めよう.
を求めよう.
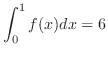 ,
,
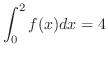 ,
,
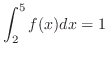 のとき,次の問いに答えよう.
のとき,次の問いに答えよう.
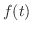 が連続であるとき,
が連続であるとき, 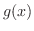 を求めよう.
を求めよう.
|
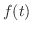 が連続であるとき,
が連続であるとき, 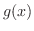 を求めよう.
を求めよう.
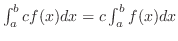 (
(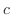 : 定数)を証明しよう.
: 定数)を証明しよう.
(3)
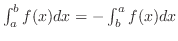 を証明しよう.
を証明しよう.
(4)
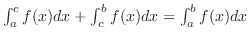 を証明しよう.
を証明しよう.
(5) ![$[a,b]$](img515.png) で
で
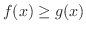 ならば,
ならば,
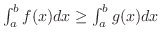 を証明しよう.
を証明しよう.