- 1.
- 次の関数の導関数を逆関数の微分法を用いて求めよう.
(a)
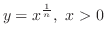 (b)
(b)
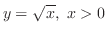
- 2.
- 次の関数の導関数を求めよう.
(a)
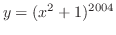 (b)
(b)
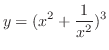 (c)
(c)
![$\displaystyle{y = [(2x+1)^{2} + (x+1)^{2}]^{3}}$](img255.png)
- 3.
-
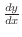 を求めよう.
を求めよう.
(a)
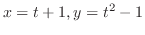 (b)
(b)
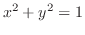
- 4.
- 次の関数の導関数を求めよう.
(a)
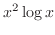 (b)
(b)
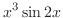 (c)
(c)
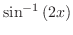 (d)
(d)
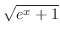 (e)
(e)
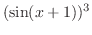 (f)
(f)
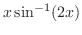
- 1.
- 次の関数の導関数を逆関数の微分法を用いて求めよう.
(a)
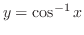 (b)
(b)
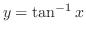
- 2.
- 次の関数の導関数を対数微分法を用いて求めよう.
(a)
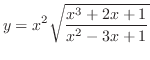 (b)
(b)
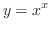 (c)
(c)
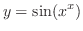 (d)
(d)
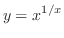
- 3.
-
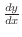 を求めよう.
を求めよう.
(a)
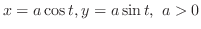 (b)
(b)
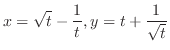
- 4.
- 次の関数の導関数を求めよう.
(a)
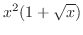 (b)
(b)
 (c)
(c)
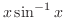 (d)
(d)
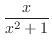 (e)
(e)
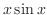
(f)
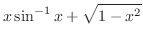 (g)
(g)
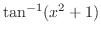 (h)
(h)
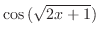
(i)
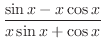 (j)
(j)
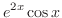 (k)
(k)
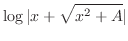 (l)
(l)
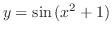 (m)
(m)
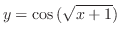 (n)
(n)
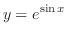
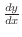 を求めよう.
を求めよう.
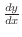 を求めよう.
を求めよう.