Next: 2.3 高次導関数 Up: 確認問題詳解 Previous: 2.1 導関数 索引
1.
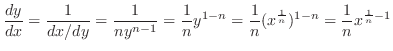
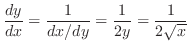
2.
(a)
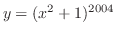 は
は
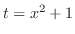 と
と
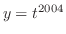 の合成関数である.したがって,合成関数の微分法より,
の合成関数である.したがって,合成関数の微分法より,
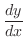 |
 |
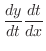 |
|
 |
 |
||
 |
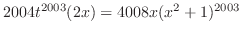 |
(b)
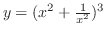 は
は
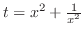 と
と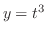 の合成関数である.したがって,合成関数の微分法より,
の合成関数である.したがって,合成関数の微分法より,
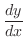 |
 |
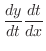 |
|
 |
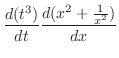 |
||
 |
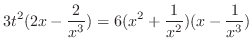 |
(c)
![$y = [(2x+1)^2 + (x+1)^2 ]^3$](img1431.png) は
は
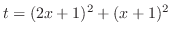 と
と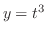 の合成関数である.したがって,合成関数の微分法より,
の合成関数である.したがって,合成関数の微分法より,
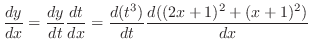
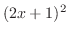 は
は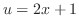 と
と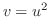 の合成関数.また,
の合成関数.また,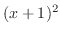 も
も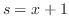 と
と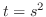 の合成関数である.したがって,
の合成関数である.したがって,
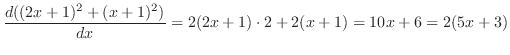
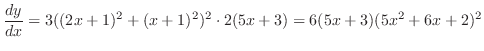
3.
(a) 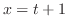 ,
,
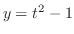 と
と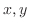 が媒介変数
が媒介変数 で与えられているので,媒介変数の微分法より
で与えられているので,媒介変数の微分法より
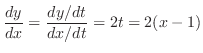
(b)
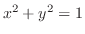 は中心
は中心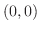 で半径1の円(単位円)を表している.そこで,極座標を用いて表すと,
で半径1の円(単位円)を表している.そこで,極座標を用いて表すと,
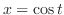 ,
,
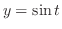 と
と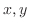 が媒介変数
が媒介変数 で表せる.したがって,媒介変数の微分法より
で表せる.したがって,媒介変数の微分法より
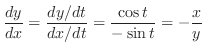
4.
 |
 |
 |
|
 |
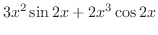 |
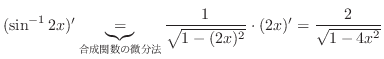
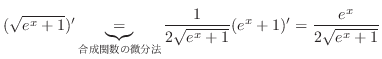
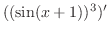 |
 |
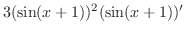 |
|
 |
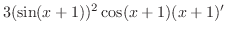 |
||
 |
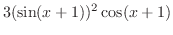 |
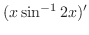 |
 |
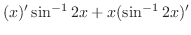 |
|
 |
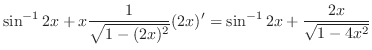 |