Next: 3.7 解答 Up: 演習問題詳解 Previous: 3.5 解答 索引
3.6
1.
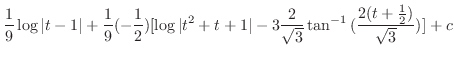 |
 |
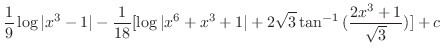 |
|
 |
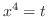 |
||
 |
![$\displaystyle 2[\frac{(1 + x)^{5/2}}{5} - \frac{(1+x)^{3/2}}{3}] + c$](img3539.png) |
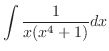 |
 |
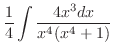 |
|
 |
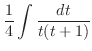 |
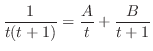 分母の次数 より
分母の次数 より
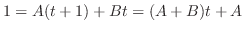
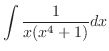 |
 |
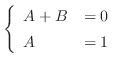 |
|
 |
![$\displaystyle 2[\frac{t^2}{2} + t + \log{\vert t-1\vert}] + c$](img3546.png) |
||
 |
 |
||
 |
 |
(c)
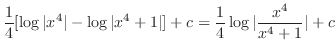 とおくと
とおくと
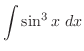 .これより
.これより
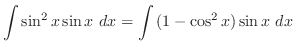 .ここで被積分関数と
.ここで被積分関数と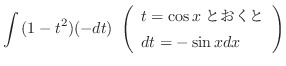 を全て
を全て の関数と
の関数と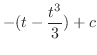 で表すと
で表すと
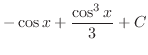
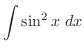 |
 |
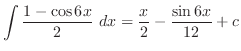 |
|
 |
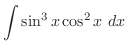 |
||
 |
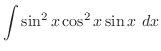 |
||
 |
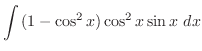 |
(d)
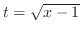 とおくと
とおくと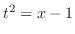 .これより
.これより
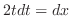 .ここで被積分関数と
.ここで被積分関数と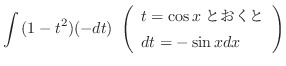 を全て
を全て の関数と
の関数と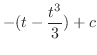 で表すと
で表すと
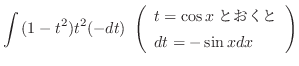
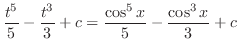 |
 |
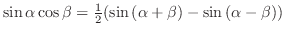 |
|
 |
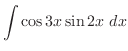 |
||
 |
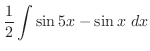 |
(e)
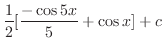 とおくと
とおくと
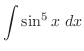 . ここで
. ここで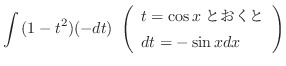 を求めるには,上の式を一旦
を求めるには,上の式を一旦 について解く必要がある.
について解く必要がある.
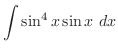 |
 |
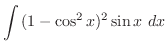 |
|
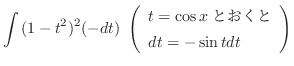 |
 |
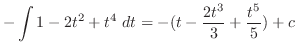 |
|
 |
 |
 |
|
 |
 |
 |
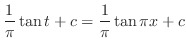 |
 |
 |
|
 |
 |
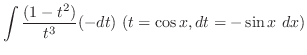 |
 |
 |
|
 |
 |
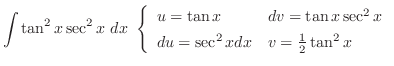
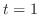 とおくと
とおくと
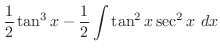
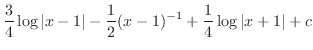 とおくと
とおくと
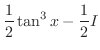
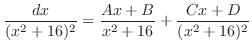 の係数を合わせると
の係数を合わせると
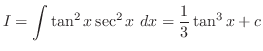
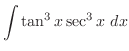 の係数を合わせると
の係数を合わせると
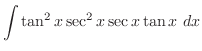
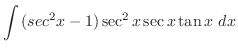
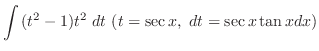 |
 |
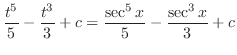 |
|
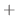 |
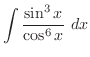 |
||
 |
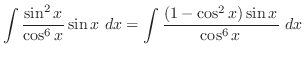 |
||
 |
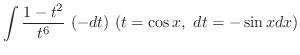 |
||
 |
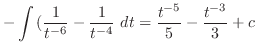 |
2.
(a)
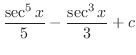 とおくと
とおくと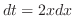 より,この問題は置換積分で求めることができる.
より,この問題は置換積分で求めることができる.
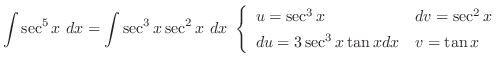 |
 |
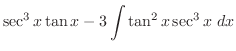 |
|
 |
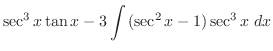 |
||
 |
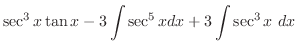 |
(b)
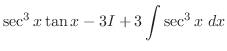 とおくと
とおくと
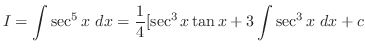 より
より
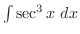 となり,全てを
となり,全てを と
と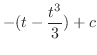 で表すと再び無理関数が登場してしまう.そこで,平方根の中が2乗の差であることに注意し,斜辺2,高さ
で表すと再び無理関数が登場してしまう.そこで,平方根の中が2乗の差であることに注意し,斜辺2,高さ ,底辺
,底辺
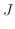 で角
で角 の直角三角形を考える.すると
の直角三角形を考える.すると
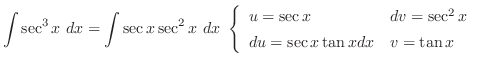 より
より
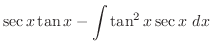 .また,
.また,
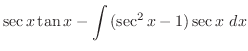
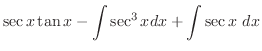 |
 |
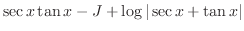 |
|
 |
![$\displaystyle 4\int{\frac{1 - \cos{2t}}{2}}\ dt = 2[t - \frac{\sin{2t}{2}}] + c$](img3608.png) |
||
 |
![$\displaystyle 2[t - \sin{t}\cos{t}] + c = 2[\sqrt{4 - x^2} - \frac{x}{2}\frac{\sqrt{4 - x^2}}{2} + c$](img3609.png) |
(c) 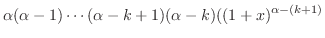 とおくと
とおくと
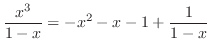 となり,全てを
となり,全てを と
と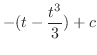 で表すことができる.
よって
で表すことができる.
よって
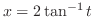 |
 |
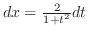 |
|
 |
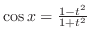 |
||
 |
![$\displaystyle \frac{1}{6}[-\log\vert 3-t\vert + \log\vert 3 + t\vert] +c = \frac{1}{6}\log\vert\frac{3+t}{3-t}\vert + c$](img3613.png) |
||
 |
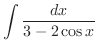 |
(d)
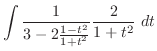 とおくと
とおくと
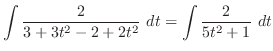 より
より
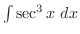 となり,全てを
となり,全てを と
と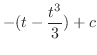 で表すと再び無理関数が登場してしまう.そこで,平方根の中が2乗の差であることに注意し,斜辺1,高さ
で表すと再び無理関数が登場してしまう.そこで,平方根の中が2乗の差であることに注意し,斜辺1,高さ ,底辺
,底辺
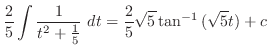 で角
で角 の直角三角形を考える.すると
の直角三角形を考える.すると
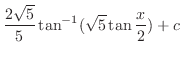 より
より
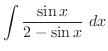 .また,
.また,
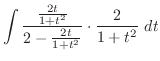
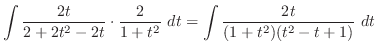 |
 |
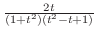 |
ここで,全ての三角関数は有理関数に直せることに注意する.特にこの場合は分子,分母とも偶数乗であるので
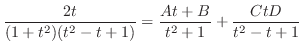 とおくと
とおくと
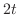 より
より
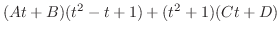 |
 |
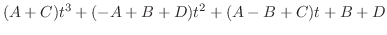 |
|
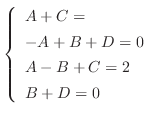 |
 |
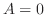 |
|
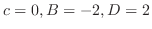 |
 |
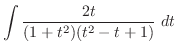 |
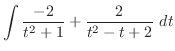 |
 |
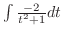 |
|
 |
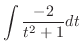 |
||
 |
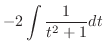 |
||
 |
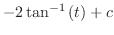 |
(e)
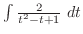 とおくと
とおくと
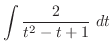 より
より
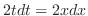 となり,全てを
となり,全てを と
と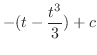 で表すと再び無理関数が登場してしまう.そこで,平方根の中が2乗の差であることに注意し,斜辺
で表すと再び無理関数が登場してしまう.そこで,平方根の中が2乗の差であることに注意し,斜辺 ,底辺
,底辺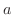 ,高さ
,高さ
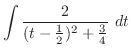 で角
で角 の直角三角形を考える.すると
の直角三角形を考える.すると
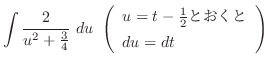 より
より
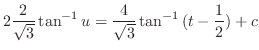 .また,
.また,

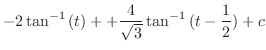 |
 |
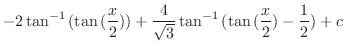 |
|
 |
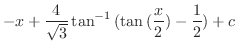 |
||
 |
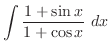 |
(f)
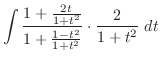 とおくと
とおくと
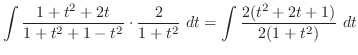 より
より
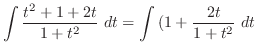 となり,全てを
となり,全てを と
と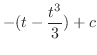 で表すと再び無理関数が登場してしまう.そこで,平方根の中が2乗の和であることに注意し,斜辺
で表すと再び無理関数が登場してしまう.そこで,平方根の中が2乗の和であることに注意し,斜辺
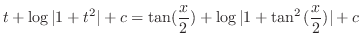 ,底辺
,底辺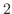 ,高さ
,高さ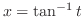 で角
で角 の直角三角形を考える.すると
の直角三角形を考える.すると
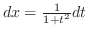 より
より
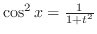 .また,
.また,
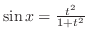
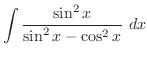 |
 |
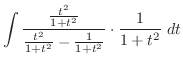 |
|
 |
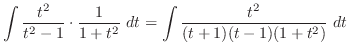 |
||
 |
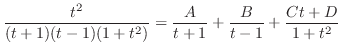 |
||
 |
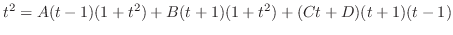 |
(g) 平方根の中が2乗の和または差になるように平方完成を行なうと
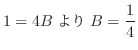
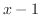 ,底辺
,底辺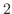 ,高さ
,高さ
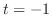 で角
で角 の直角三角形を考える.すると
の直角三角形を考える.すると
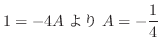 より
より
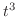 .また,
.また,
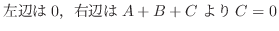
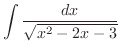 |
 |
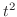 |
|
 |
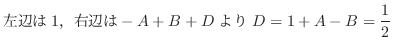 |
||
 |
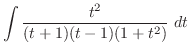 |
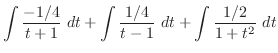 を用いたが,公式を用いなくとも次のように積分できる.
を用いたが,公式を用いなくとも次のように積分できる.
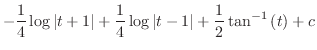 |
 |
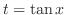 |
|
 |
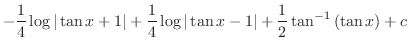 |
||
 |
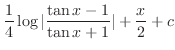 |
||
 |
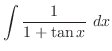 |
(h) 平方根の中が2乗の和または差になるように平方完成を行なうと
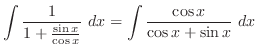
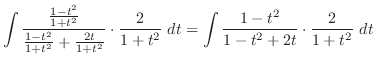 ,底辺
,底辺
 ,高さ
,高さ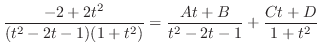 で角
で角 の直角三角形を考える.すると
の直角三角形を考える.すると
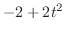 より
より
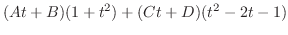 .また,
.また,
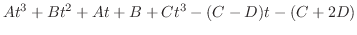
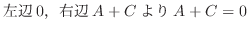 |
 |
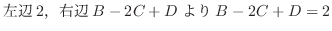 |
|
 |
![$\displaystyle -\int{3 - 3\sin{t}}\ dt = -[3t + 3\cos{t}] + c$](img3682.png) |
||
 |
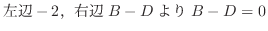 |
||
 |
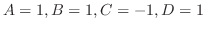 |
(i) 平方根の中が2乗の和または差になるように平方完成を行なうと
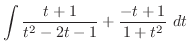
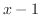 ,底辺
,底辺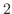 ,高さ
,高さ
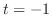 で角
で角 の直角三角形を考える.すると
の直角三角形を考える.すると
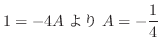 より
より
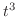 .また,
.また,
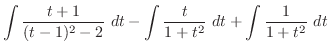
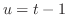 |
 |
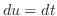 |
|
 |
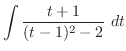 |
||
 |
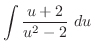 |
||
 |
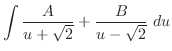 |
||
 |
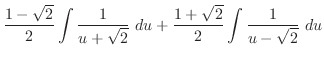 |
(j) 平方根の中が2乗の和または差になるように平方完成を行なうと
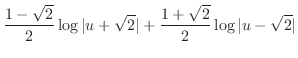
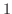 ,底辺
,底辺
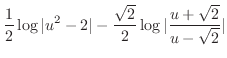 ,高さ
,高さ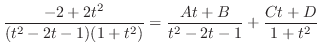 で角
で角 の直角三角形を考える.すると
の直角三角形を考える.すると
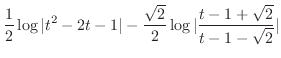 より
より
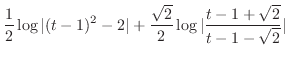 .また,
.また,
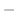
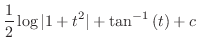 |
 |
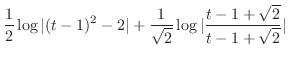 |
|
 |
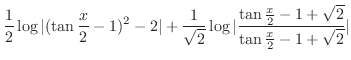 |
||
 |
![$\displaystyle -\int{\frac{1 + \cos{t}}{2}}\ dt = -[\frac{t}{2} + \frac{\sin{2t}}{4}] + c$](img3701.png) |
||
 |
![$\displaystyle -[\frac{t}{2} + \frac{\sin{t}\cos{t}}{2}] + c$](img3702.png) |
||
 |
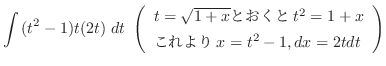 |
(k) 平方根の中が2乗の和または差になるように平方完成を行なうと
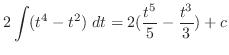
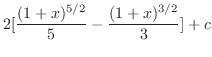 ,底辺
,底辺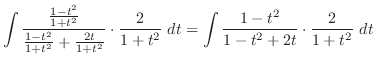 ,高さ
,高さ
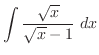 で角
で角 の直角三角形を考える.すると
の直角三角形を考える.すると
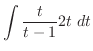 より
より
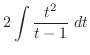 .また,
.また,
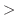
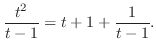 |
 |
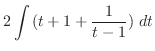 |
|
 |
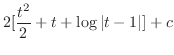 |
||
 |
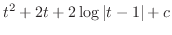 |
ここで,全ての三角関数は有理関数に直せることに注意する.
まず,
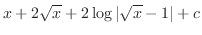 の積分を行なう.
この場合は分子,分母とも偶数乗であるので
の積分を行なう.
この場合は分子,分母とも偶数乗であるので
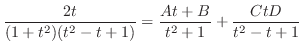 とおくと
とおくと
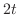 より
より
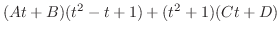 |
 |
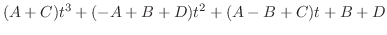 |
|
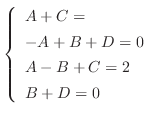 |
 |
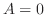 |
|
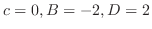 |
 |
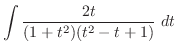 |
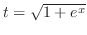 |
 |
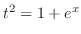 |
|
 |
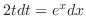 |
||
 |
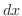 |
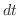 の積分を行なう.この場合,分母に奇数乗を含んでいるので,分母と分子に
の積分を行なう.この場合,分母に奇数乗を含んでいるので,分母と分子に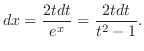 をかける.すると
をかける.すると
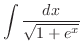 |
 |
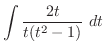 |
|
 |
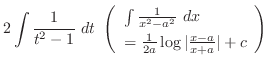 |
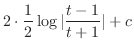 とおくと
とおくと
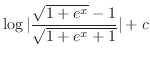 となるので
となるので
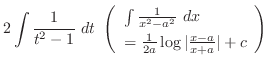 |
 |
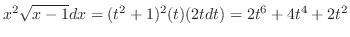 |
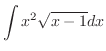
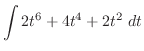
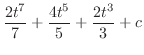 とおくと
とおくと
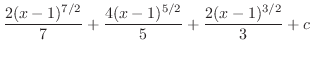
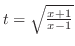 とおくと
とおくと
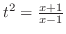
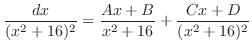 の係数を合わせると
の係数を合わせると
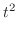
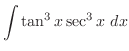 の係数を合わせると
の係数を合わせると
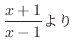
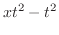
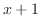 |
 |
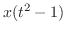 |
|
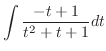 |
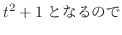 |
||
 |
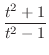 |
||
 |
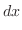 |
||
 |
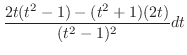 |
||
 |
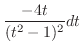 |
したがって,
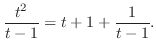 |
 |
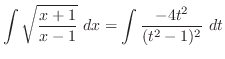 |
|
 |
![$\displaystyle 27[\frac{\tan^{3}{t}}{3} + \frac{1}{4}\log\vert\frac{1-\sin{t}}{1+\sin{t}}\vert + \frac{1}{4}(\frac{2\sin{t}}{1-\sin^{2}{t}}) ]+ c$](img3744.png) |
||
 |
![$\displaystyle 27[\frac{1}{3}(\frac{\sqrt{x^2 + 6x}}{3})^{3} + \frac{1}{4}\log\v...
...(\frac{2\frac{\sqrt{x^2 + 6x}}{x+3}}{1-(\frac{\sqrt{x^2 + 6x}}{x+3})^{2}})] + c$](img3745.png) |