Next: 3.6 解答 Up: 演習問題詳解 Previous: 3.4 解答 索引
3.5
1.
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
 |
 |
 |
|
 |
![$\displaystyle \frac{1}{2}[\frac{-\cos{5x}}{5} + \cos{x}] + c$](img3399.png) |
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
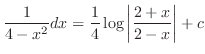 |
 |
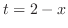 |
|
 |
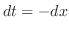 |
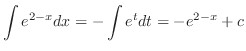 |
 |
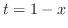 |
|
 |
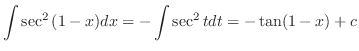 |
||
 |
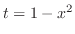 |
||
 |
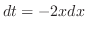 |
||
 |
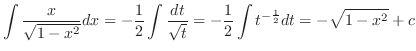 |
 |
 |
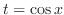 |
|
 |
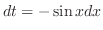 |
||
 |
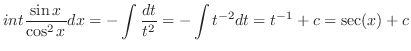 |
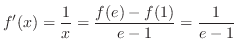 は
は
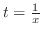
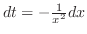 |
 |
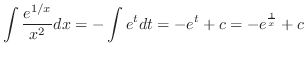 |
|
 |
 |
||
 |
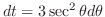 |
||
 |
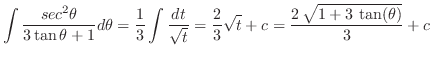 |
別解
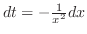 |
 |
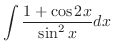 |
|
 |
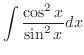 |
||
 |
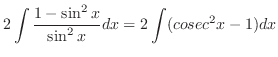 |
||
 |
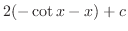 |
||
 |
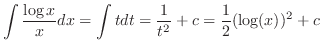 |
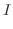 |
 |
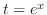 |
|
 |
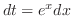 |
||
 |
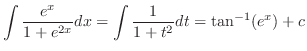 |
||
 |
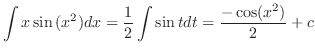 |
||
 |
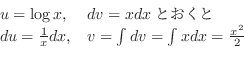 |
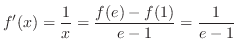 は
は
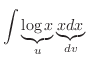
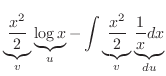 を求めればよい.
を求めればよい.
 |
 |
 |
|
 |
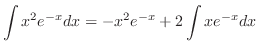 |
||
 |
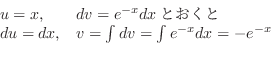 |
||
 |
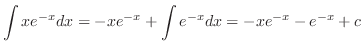 |
||
 |
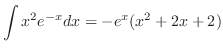 |
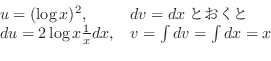
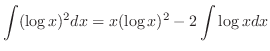
(k)
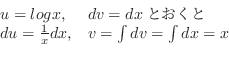 とおくと,
とおくと,
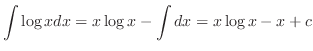 ,
,
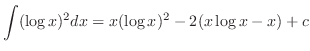 ,
,
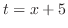 となるので,全ての三角関数は有理関数に直せる.
となるので,全ての三角関数は有理関数に直せる.
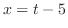 |
 |
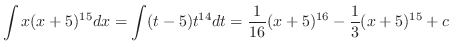 |
|
 |
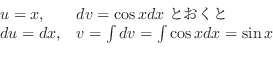 |
||
 |
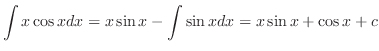 |
||
 |
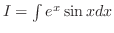 |
(l)
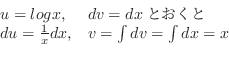 とおくと,
とおくと,
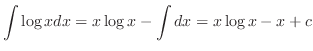 ,
,
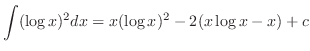 ,
,
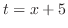 となるので,全ての三角関数は有理関数に直せる.
となるので,全ての三角関数は有理関数に直せる.
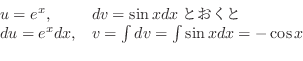 |
 |
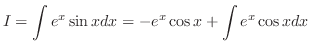 |
|
 |
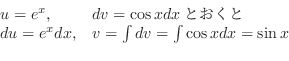 |
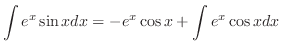 を部分分数分解すると
を部分分数分解すると
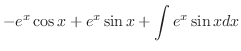
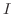 |
 |
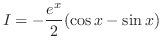 |
|
 |
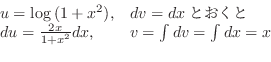 |
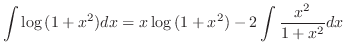
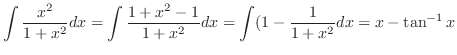 を得る.またこれより,
を得る.またこれより,
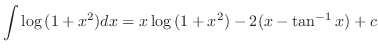 を得る.したがって,
を得る.したがって,
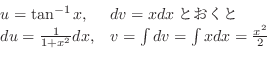 |
 |
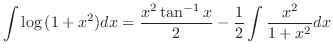 |
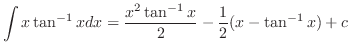 を求める.
を求める.
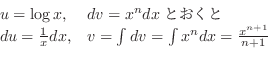 |
 |
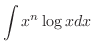 |
|
 |
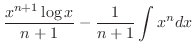 |
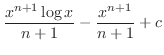 を求める.
を求める.
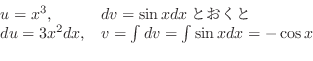 |
 |
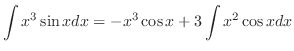 |
|
 |
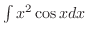 |
||
 |
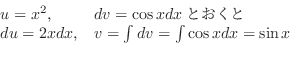 |
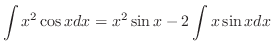 を代入すると
を代入すると
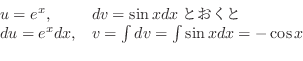 |
 |
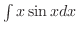 |
|
 |
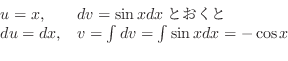 |
||
 |
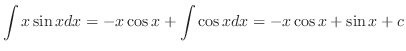 |
(m)
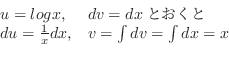 とおくと,
とおくと,
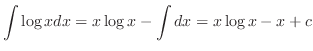 ,
,
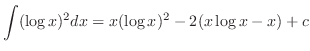 ,
,
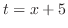 となるので,全ての三角関数は有理関数に直せる.
となるので,全ての三角関数は有理関数に直せる.
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
(n)
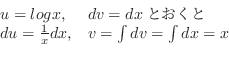 とおいてもよいが,被積分関数は全て2乗されているので,
とおいてもよいが,被積分関数は全て2乗されているので,
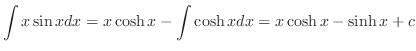 おくと,
おくと,
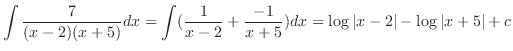 ,
,
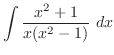 ,
,
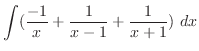 となる.
となる.
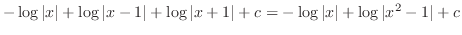 |
 |
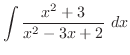 |
|
 |
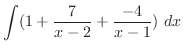 |
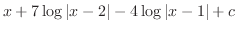
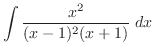
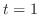 とおくと
とおくと
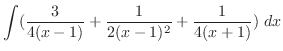
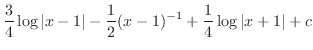 とおくと
とおくと
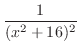
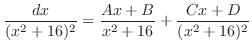 の係数を比較すると
の係数を比較すると
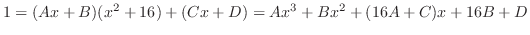
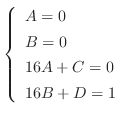 の係数を比較すると
の係数を比較すると
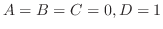
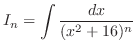 |
 |
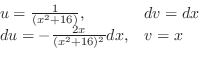 |
|
 |
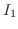 |
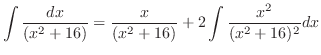 に注意すると
に注意すると
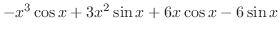 |
 |
 |
|
 |
 |
(o)
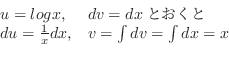 とおくと,
とおくと,
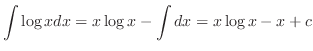 ,
,
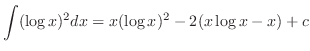 ,
,
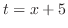 となるので,全ての三角関数は有理関数に直せる.
となるので,全ての三角関数は有理関数に直せる.
 |
 |
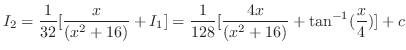 |
|
 |
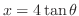 |
||
 |
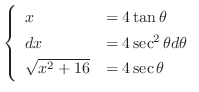 |
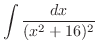
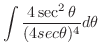 |
 |
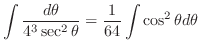 |
|
 |
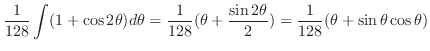 |
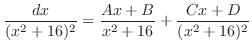 の係数は
の係数は
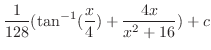
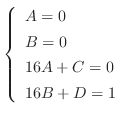 の係数は
の係数は
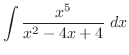
 の係数は
の係数は
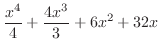
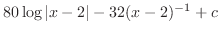
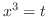
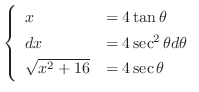 |
 |
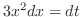 |
|
 |
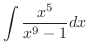 |
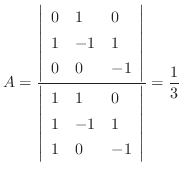
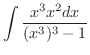 とおくと
とおくと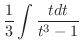 より,
より,
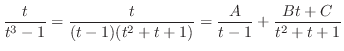 |
 |
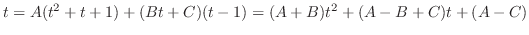 |
|
 |
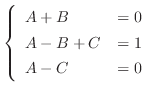 |
||
 |
 |
||
 |
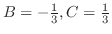 |
||
 |
 |
||
 |
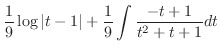 |
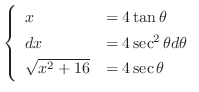 |
 |
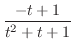 |
|
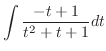 |
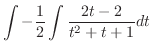 |
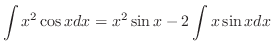 を代入して完成.
を代入して完成.
 |
 |
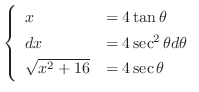 |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |