Next: 6.4 全微分 Up: 確認問題詳解 Previous: 6.2 偏導関数 索引
1.
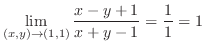
(b)
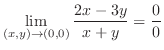 の不定形.そこで,分子の最小次数と分母の最小次数を比較すると同じ.この場合,極限値が存在しない可能性が高いので,反例を見つける.
の不定形.そこで,分子の最小次数と分母の最小次数を比較すると同じ.この場合,極限値が存在しない可能性が高いので,反例を見つける.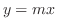 とおくと,
とおくと,
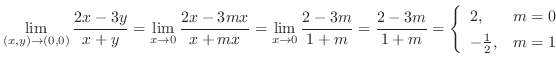
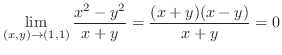
2.
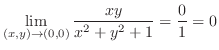
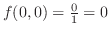 より,
より,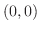 で連続.
で連続.
(b)
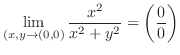 の不定形.ここで,分子の最小次数は2で分母の最小次数も2であることから,極限値の存在する可能性は低い.極限値が存在しないことを示すには,反例を挙げればよい.
の不定形.ここで,分子の最小次数は2で分母の最小次数も2であることから,極限値の存在する可能性は低い.極限値が存在しないことを示すには,反例を挙げればよい.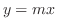 とおくと,
とおくと,
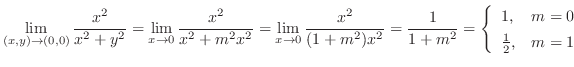
(c)
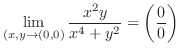 の不定形.ここで,分子の最小次数は3で分母の最小次数は2であることから,極限値の存在する可能性は高い.そこで,
の不定形.ここで,分子の最小次数は3で分母の最小次数は2であることから,極限値の存在する可能性は高い.そこで,
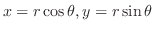 とおくと,
とおくと,
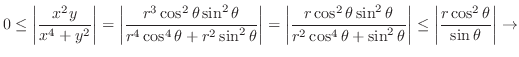
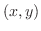 が
が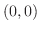 に近づいても同じ値に近づくので,
に近づいても同じ値に近づくので,
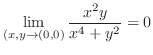 また,
また,
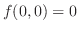 より,
より,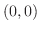 で連続.
で連続.