Next: 6.3 関数の極限 Up: 確認問題詳解 Previous: 6.1 関数の定義 索引
1.
(a)  での偏微分は
での偏微分は 以外の変数をすべて定数と見なして微分すればよいので,
以外の変数をすべて定数と見なして微分すればよいので,
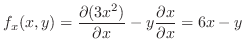
 での偏微分は
での偏微分は 以外の変数をすべて定数と見なして微分すればよいので,
以外の変数をすべて定数と見なして微分すればよいので,
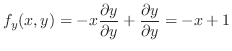
(b)  での偏微分は
での偏微分は 以外の変数をすべて定数と見なして微分すればよいので,
以外の変数をすべて定数と見なして微分すればよいので,
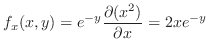
 での偏微分は
での偏微分は 以外の変数をすべて定数と見なして微分すればよいので,
以外の変数をすべて定数と見なして微分すればよいので,
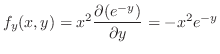
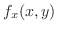 |
 |
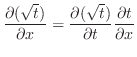 |
|
 |
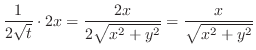 |
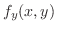 |
 |
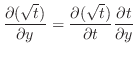 |
|
 |
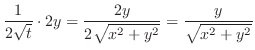 |
(d)  での偏微分は
での偏微分は 以外の変数をすべて定数と見なして微分すればよいので,
以外の変数をすべて定数と見なして微分すればよいので,
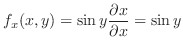
 での偏微分は
での偏微分は 以外の変数をすべて定数と見なして微分すればよいので,
以外の変数をすべて定数と見なして微分すればよいので,
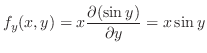
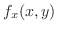 |
 |
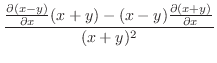 |
|
 |
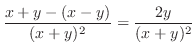 |
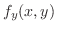 |
 |
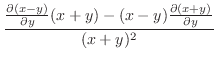 |
|
 |
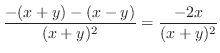 |
2.
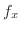 |
 |
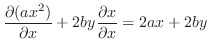 |
|
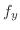 |
 |
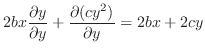 |
|
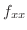 |
 |
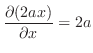 |
|
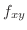 |
 |
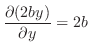 |
|
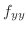 |
 |
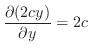 |
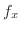 |
 |
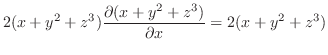 |
|
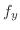 |
 |
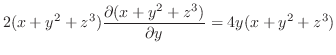 |
|
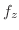 |
 |
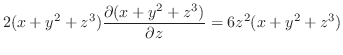 |
|
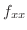 |
 |
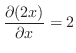 |
|
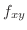 |
 |
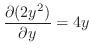 |
|
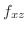 |
 |
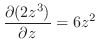 |
|
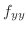 |
 |
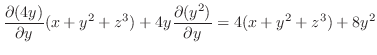 |
|
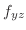 |
 |
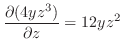 |
|
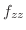 |
 |
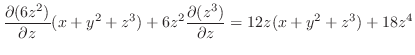 |
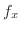 |
 |
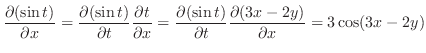 |
|
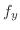 |
 |
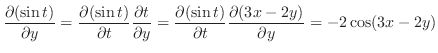 |
|
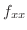 |
 |
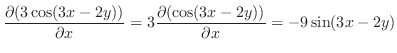 |
|
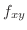 |
 |
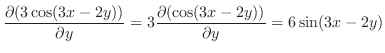 |
|
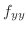 |
 |
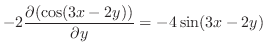 |
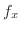 |
 |
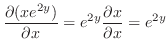 |
|
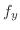 |
 |
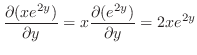 |
|
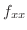 |
 |
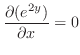 |
|
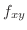 |
 |
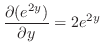 |
|
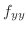 |
 |
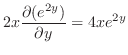 |