Next: 6.2 偏導関数 Up: 確認問題詳解 Previous: 5.2 曲線 索引
1.
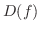 |
 |
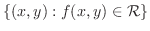 |
|
 |
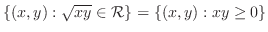 |
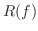 |
 |
 |
|
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
|
 |
 |
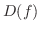 |
 |
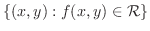 |
|
 |
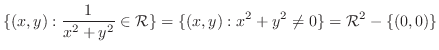 |
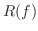 |
 |
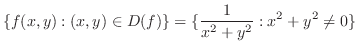 |
|
 |
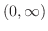 |
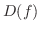 |
 |
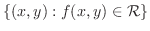 |
|
 |
 |
 |
 |
 |
|
 |
![$\displaystyle [0,1]$](img2259.png) |
 |
 |
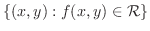 |
|
 |
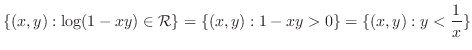 |
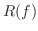 |
 |
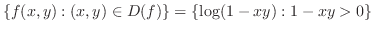 |
|
 |
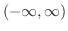 |
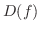 |
 |
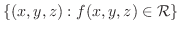 |
|
 |
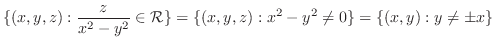 |
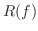 |
 |
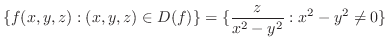 |
|
 |
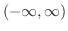 |
2.
(a)
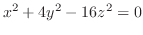 は
は
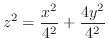 と書き直せる.
と書き直せる.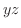 平面でのトレースは
平面でのトレースは
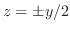 ,
, 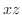 平面でのトレースは
平面でのトレースは
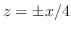 .等位面でのトレースは楕円となる.したがって,2次錐面.別名円錐.
.等位面でのトレースは楕円となる.したがって,2次錐面.別名円錐.
(b)
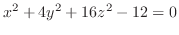 は
は
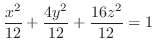 と書き直せる.
と書き直せる.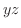 平面でのトレースは楕円
平面でのトレースは楕円
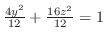 ,
, 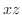 平面でのトレースは楕円
平面でのトレースは楕円
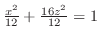 .等位面でのトレースも楕円となる.したがって,楕円面.
.等位面でのトレースも楕円となる.したがって,楕円面.
(c)
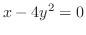 は放物線
は放物線
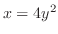 が
が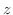 軸に平行にのびている.したがって,放物柱.
軸に平行にのびている.したがって,放物柱.
(d)
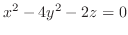 .
. 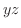 平面でのトレースは放物線
平面でのトレースは放物線
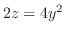 ,
, 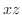 平面でのトレースは放物線
平面でのトレースは放物線
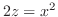 .等位面でのトレースは双曲線.したがって,双曲放物面
.等位面でのトレースは双曲線.したがって,双曲放物面
(e)
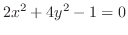 は楕円
は楕円
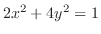 が
が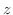 軸に平行にのびている.したがって, 楕円柱.
軸に平行にのびている.したがって, 楕円柱.
(f)
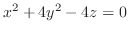 .
. 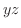 平面でのトレースは放物線
平面でのトレースは放物線
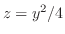 ,
, 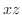 平面でのトレースは放物線
平面でのトレースは放物線
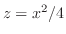 .等位面でのトレースは楕円.したがって,楕円放物面
(g)
.等位面でのトレースは楕円.したがって,楕円放物面
(g)
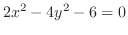 は双曲線
は双曲線
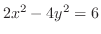 が
が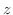 軸に平行にのびている.したがって, 双曲柱.
軸に平行にのびている.したがって, 双曲柱.
(h)
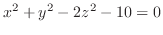 .
. 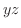 平面でのトレースは双曲線
平面でのトレースは双曲線
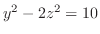 ,
, 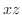 平面でのトレースは双曲線
平面でのトレースは双曲線
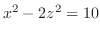 .等位面でのトレースは楕円.したがって,1葉双曲面
.等位面でのトレースは楕円.したがって,1葉双曲面
(i)
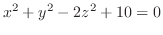 .
. 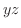 平面でのトレースは双曲線
平面でのトレースは双曲線
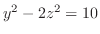 ,
, 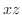 平面でのトレースは双曲線
平面でのトレースは双曲線
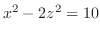 .
.
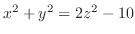 より 等位面でのトレースは
より 等位面でのトレースは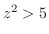 のときつまり
のときつまり
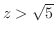 または
または
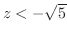 のとき楕円.したがって,2葉双曲面
のとき楕円.したがって,2葉双曲面