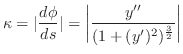Next: 6.1 関数の定義 Up: 確認問題詳解 Previous: 5.1 ベクトル関数 索引
1.
(a) ベクトル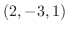 に平行より,求める直線の方向ベクトルは
に平行より,求める直線の方向ベクトルは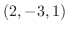 .この直線は点
.この直線は点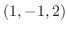 を通るので,求める直線のベクトル方程式は
を通るので,求める直線のベクトル方程式は
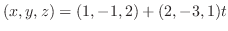
(b) 線分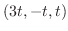 に平行より,求める直線の方向ベクトルは
に平行より,求める直線の方向ベクトルは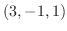 .この直線は点
.この直線は点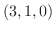 を通るので,求める直線のベクトル方程式は
を通るので,求める直線のベクトル方程式は
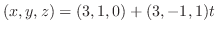
(c) 2点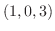 と
と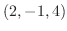 を通るので,求める直線の方向ベクトルは
を通るので,求める直線の方向ベクトルは
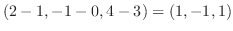 .この直線は点
.この直線は点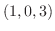 を通るので,求める直線のベクトル方程式は
を通るので,求める直線のベクトル方程式は
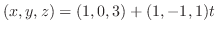
2.
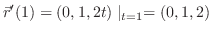
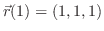 より,接線の方程式は
より,接線の方程式は
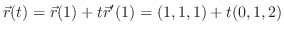
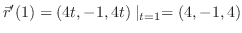
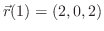 より,接線の方程式は
より,接線の方程式は
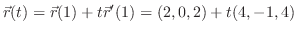
3.
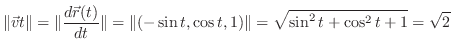
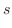 |
 |
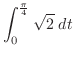 |
|
 |
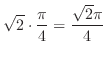 |
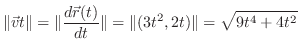
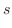 |
 |
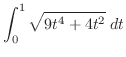 |
|
 |
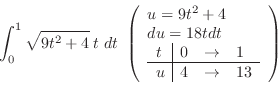 |
||
 |
![$\displaystyle \int_{4}^{13}\sqrt{u}\frac{du}{18} = \frac{1}{18}\cdot \frac{2}{3}[u^{3/2}]_{4}^{13}$](img2232.png) |
||
 |
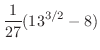 |
4.
曲率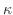 は曲線の曲がり具合を表したものである.曲線の曲がり具合は曲線の接線が
は曲線の曲がり具合を表したものである.曲線の曲がり具合は曲線の接線が 軸と作る角
軸と作る角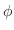 が曲線上を
が曲線上を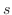 だけ動くときにどれだけ変化するかを調べることにより分かる.
これより,
だけ動くときにどれだけ変化するかを調べることにより分かる.
これより,