オイラー e(Euler e)と超越関数
- 1.
- 次の漸化式で定義される数列
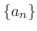 は収束するか判定しよう.また,収束する場合は,極限値を求めよう.
は収束するか判定しよう.また,収束する場合は,極限値を求めよう.
(a)
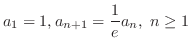 (b)
(b)
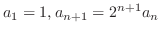
(c)
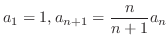
- 2.
- 表より,次の値を求めよう.
- 3.
- 次の方程式の解を求めよう.
(a)
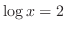 (b)
(b)
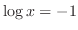 (c)
(c)
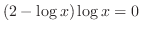
(d)
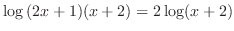
- 1.
- 次の数列は有界か調べよう.
(a)
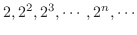 (b)
(b) 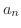 は
は 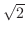 の小数第
の小数第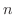 位までとった近似値.
位までとった近似値.
- 2.
- 次の漸化式で定義される数列
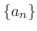 の極限値を求めよう.
の極限値を求めよう.
(a)
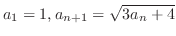 (b)
(b)
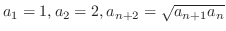
- 3.
- 次の数列の極限値を求めよう.
(a)
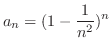 (b)
(b)
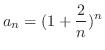 (c)
(c)
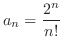
(d)
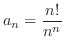
- 4.
- 次の極限値を求めよう.
(a)
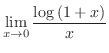 (b)
(b)
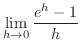 (c)
(c)
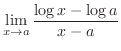
(d)
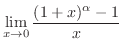 (e)
(e)
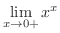
- 5.
- 算術平均
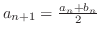 と幾何平均
と幾何平均
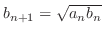 で定義された数列
で定義された数列
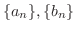 について以下の問に答えよう.
について以下の問に答えよう.
(a) 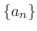 と
と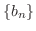 は収束することを示そう.
は収束することを示そう.
(b)
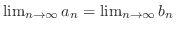 を示そう.
を示そう.
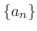 の極限値を求めよう.
の極限値を求めよう.
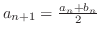 と幾何平均
と幾何平均
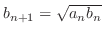 で定義された数列
で定義された数列
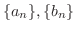 について以下の問に答えよう.
について以下の問に答えよう.
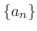 と
と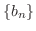 は収束することを示そう.
は収束することを示そう.
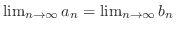 を示そう.
を示そう.