Next: 1.7 解答 Up: 演習問題詳解 Previous: 1.5 解答 索引
1.6
1.
(a)どんな整数 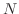 を選んでも
を選んでも
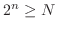 となる番号
となる番号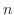 が存在する.よって非有界
が存在する.よって非有界
(b)
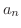 は
は 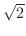 の第
の第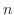 位までを表わしているので,
位までを表わしているので,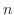 がどんなに大きくなっても
がどんなに大きくなっても 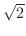 より大きくなれない.よって有界
より大きくなれない.よって有界
2.
(a)
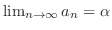 とおくと
とおくと
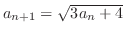 より
より
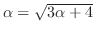 となる. そこで両辺を2乗すると
となる. そこで両辺を2乗すると
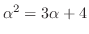 となるので,
となるので,
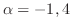 . 条件
. 条件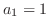 より
より
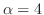 と考えられる.次に
と考えられる.次に
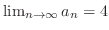 であることを示す. 定理1.13より
であることを示す. 定理1.13より
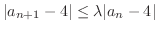 となる
となる
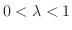 が存在することを示せばよい.
が存在することを示せばよい.
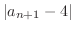 |
 |
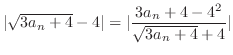 |
|
 |
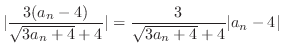 |
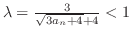
3.
![$\displaystyle \lim_{n \to \infty}(1 + \frac{2}{n})^{n} = \lim_{m \to \infty}[(1 + \frac{1}{m})^{m}]^{2} = e^{2} $](img3128.png)
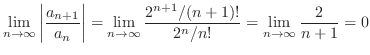
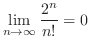
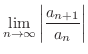 |
 |
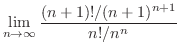 |
|
 |
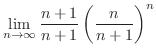 |
||
 |
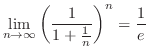 |
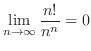
4.
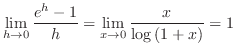
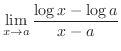 |
 |
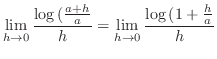 |
|
 |
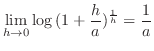 |
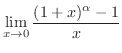 |
 |
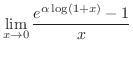 |
|
 |
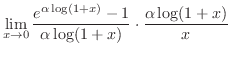 |
||
 |
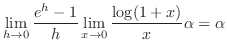 |
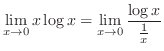
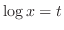 とおくと
とおくと 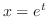 . よって 例題1.32より
. よって 例題1.32より
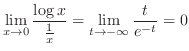 .これより,
.これより,
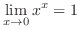
5.
(a)
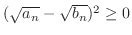 より,
より,
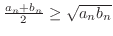 . したがって,
. したがって,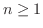 において
において
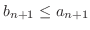 が成り立つ.ということは,
が成り立つ.ということは,
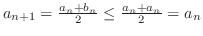 .また,
.また,
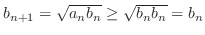 .これより,
.これより,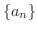 は下に有界な単調減少数列で
は下に有界な単調減少数列で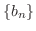 は上に有界な単調増加数列となり収束する.
は上に有界な単調増加数列となり収束する.
(b)
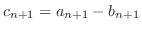 とおくと,すべての
とおくと,すべての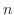 で
で
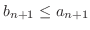 より,
より,
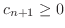 . また,
. また,
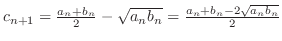 . ここで,
. ここで,
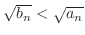 より,両辺に
より,両辺に
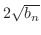 をかけると,
をかけると,
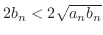 となる.これより,
となる.これより,
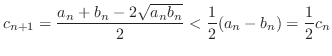
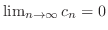 となり,
となり,
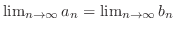 .
.