Next: 平均値の定理と関数の性質(mean-value theorem and properties Up: 微分法(DIFFERENTIATION) Previous: 微分法(Differentiation Formulas) 目次 索引
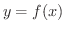 の導関数
の導関数
 が微分可能ならば,その導関数
が微分可能ならば,その導関数
 が考えられます.これを
が考えられます.これを 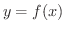 の 第2次導関数(2nd derivative) といい,
の 第2次導関数(2nd derivative) といい,

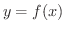 を次々に
を次々に  回微分することにより第n次導関数(nth derivative)が定義されます.第n次導関数
回微分することにより第n次導関数(nth derivative)が定義されます.第n次導関数
 が存在するとき,
が存在するとき,  は n回微分可能(n times differentiable) であるといいます.さらに,
は n回微分可能(n times differentiable) であるといいます.さらに,
 が連続のとき,
が連続のとき,  級であるといいます.また,すべての自然数
級であるといいます.また,すべての自然数  について
について
 が存在するとき,無限回微分可能(infinitely many times differentiable)あるいは
が存在するとき,無限回微分可能(infinitely many times differentiable)あるいは
 級であるといいます.
級であるといいます.

解答 物体を地表面の近くで自然落下させ,空気抵抗がほとんどないとすると,時刻 における物体の位置
における物体の位置 はGalileoの公式より,
はGalileoの公式より,

 より,
より, は時刻
は時刻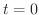 の時の物体の高さを表します.これを初期位置(initial position)といいます.この関数を微分すると,
の時の物体の高さを表します.これを初期位置(initial position)といいます.この関数を微分すると,

 より,
より, は時刻
は時刻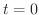 の時の物体の速度を表します.これを初速度(initial velocity)といいます.第2次導関数を求めると,
の時の物体の速度を表します.これを初速度(initial velocity)といいます.第2次導関数を求めると,

 より,
より, は時刻
は時刻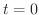 の時の物体の加速度を表します.ここでの負の符号は方向を表しています.定数
の時の物体の加速度を表します.ここでの負の符号は方向を表しています.定数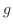 を重力加速度定数(gravitational constant)といいます.
を重力加速度定数(gravitational constant)といいます.

第n次導関数に関して次の定理が成り立ちます.
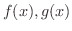 が
が  級のとき,次の公式が成り立つ.
級のとき,次の公式が成り立つ.

 (c : 定数)
(c : 定数)


上の定理の(3)は Leibnizの定理(Leibniz theorem) といい,
 は
は
 を表わします(例題1.6参照).
を表わします(例題1.6参照).
証明 (3)の証明

 のときに成り立ちます.次に
のときに成り立ちます.次に  のときに成り立つと仮定し,
のときに成り立つと仮定し,  のときを考えましょう.
のときを考えましょう.
 |
 |
![$\displaystyle [(f(x)g(x))^{(k)}]^{\prime} = [ \sum_{i=0}^{k}\binom{k}{i}f^{(k-i)}(x)g^{(i)}(x)]^{\prime}$](img1475.png) |
|
 |
 |
 |
 |
![$\displaystyle [(f(x)g(x))^{(k)}]^{\prime} = [ \sum_{i=0}^{k}\binom{k}{i}f^{(k-i)}(x)g^{(i)}(x)]^{\prime}$](img1475.png) |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |


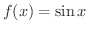 (2)
(2)

解
(1)
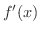 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
 が帰納法で示せます.
が帰納法で示せます.

(2)  とおくと,
とおくと,
 定数.したがって,
定数.したがって,

 の第n次導関数を求めてみましょう.
の第n次導関数を求めてみましょう.
解 まず,

 と
と
 の第n次導関数を計算するのがよい.
の第n次導関数を計算するのがよい.
 より,
より,
 となることが帰納法により示せる.次に,
となることが帰納法により示せる.次に,
 を考える.
を考える. とおくと,
とおくと,
 定数より,
定数より,


 の第n次導関数を求めてみましょう.
の第n次導関数を求めてみましょう.
解
 とおくと,
とおくと,

 |
 |
 |
|
 |
 |