Next: 高次導関数(higher-order derivatives) Up: 微分法(DIFFERENTIATION) Previous: 導関数(derivatives) 目次 索引
微分公式を学んだだけでも,かなりの関数の導関数を求めることができるようになりました.しかし,
 のような関数の導関数を求めるとき,積の微分法を用いて,微分していたら大変面倒です.そこで一工夫をしてみましょう.まず,
のような関数の導関数を求めるとき,積の微分法を用いて,微分していたら大変面倒です.そこで一工夫をしてみましょう.まず,
 を分解すると
を分解すると
 は
は
 と
と
 の合成関数でできていることがわかります.そこで
の合成関数でできていることがわかります.そこで  の微分
の微分  と
と  の微分
の微分  を求めると,
を求めると,


 がそれぞれ
がそれぞれ の関数として微分可能ならば,合成関数
の関数として微分可能ならば,合成関数
 も
も  の関数として微分可能で,
の関数として微分可能で,

証明
 とすると,
とすると,
ここで,
 のとき,
のとき,
 に注意する.
に注意する.
 のとき,
のとき,
 とおくと,
とおくと,
 のとき,
のとき,
 となり,
となり,
 とすると,式(2.1)より
とすると,式(2.1)より
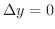 となるので,この場合は
となるので,この場合は
 と定義する.この結果,式(2.2)は
と定義する.この結果,式(2.2)は
 でも
でも
 でも成り立つ.
式(2.2)を
でも成り立つ.
式(2.2)を
 で割り,
で割り,
 とすると,
とすると,
 |
 |
 |
|
 |
 |

 を微分してみましょう.
を微分してみましょう.
解
まず,
 を分解すると
を分解すると
 と
と
 となります.よって
となります.よって


 整数 を微分してみましょう.
整数 を微分してみましょう.
解
まず,両辺を  乗すると
乗すると

 について微分すると,左辺は
について微分すると,左辺は





 のように
のように
 の逆関数の導関数を求める必要もでてきます.そんなとき,もとの関数
の逆関数の導関数を求める必要もでてきます.そんなとき,もとの関数
 の導関数を使えるような気がします.実際,逆関数の導関数を求めるときには,次の微分法を用います.
の導関数を使えるような気がします.実際,逆関数の導関数を求めるときには,次の微分法を用います.
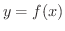 は微分可能で
は微分可能で
 とする.もし,
とする.もし, 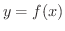 の逆関数
の逆関数
 が存在するならば,
が存在するならば,

証明
 とおくと
とおくと


 の導関数を求めてみましょう.
の導関数を求めてみましょう.
解
まず,
 とは,
とは,
 で
で  の主値が
の主値が
 ,
,
 のことでした.ここで
のことでした.ここで 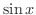 の導関数なら知っているので,
の導関数なら知っているので,
 の両辺を
の両辺を  について微分すると,
について微分すると,

 では
では
 であるので,
であるので,



 の導関数も求めてみましょう.
の導関数も求めてみましょう.
解
まず 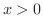 のときを考えてみましょう.
のときを考えてみましょう.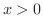 のとき,
のとき,


次に,  のとき,
のとき,
 .そこで
.そこで  とおくと,
とおくと,  となり,合成関数の微分法より
となり,合成関数の微分法より



対数微分法
関数が複雑な形で与えられているとき,微分を行う前に少し簡単な形に直しておきたいことがあります.そんなときに用いると便利なものに対数微分法とよばれるものがあります.
 を微分してみましょう.
を微分してみましょう.
解 まず,両辺に対数をとると,

 で微分すると例題2.2より
で微分すると例題2.2より
 |
 |
 |
|
 |
 |
 |
 |
 |
|
 |
 |
このように両辺の対数をとって微分する方法を 対数微分法(logarithmic differentiation) といいます.
 の
の  が整数のときの導関数は,例題2.1 で求めました.しかし,
が整数のときの導関数は,例題2.1 で求めました.しかし,
 の
の 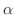 が実数のときの導関数は例題2.1 で用いた方法では求められません(なぜでしょう?).しかしもう大丈夫です.なぜなら私たちには対数微分法があるからです.
が実数のときの導関数は例題2.1 で用いた方法では求められません(なぜでしょう?).しかしもう大丈夫です.なぜなら私たちには対数微分法があるからです.
 の導関数を求めてみましょう.
の導関数を求めてみましょう.
解 両辺の対数をとると.

 で微分すると,
で微分すると,


 の導関数は
の導関数は  のときと同じ形をとることがわかりました.
のときと同じ形をとることがわかりました.

ここまでの例題で求めた導関数は微分計算の基礎となるものです.次の例題の後にまとめておきますので,活用して下さい.
単位円上の点 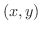 を
を
 と表わし
と表わし 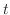 を時間と考えれば
を時間と考えれば
 は時刻
は時刻 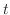 における物体の位置と考えられます.このときの
における物体の位置と考えられます.このときの 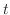 のことを 媒介変数(parameter)
といいます.このように媒介変数を用いて表わされた関数の微分を行うには,次のような方法があります.
のことを 媒介変数(parameter)
といいます.このように媒介変数を用いて表わされた関数の微分を行うには,次のような方法があります.
 がともに区間
がともに区間 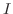 で微分可能で,しかも
で微分可能で,しかも
 であるならば,
であるならば,  は
は  に関して微分可能で,次の式が成り立つ.
に関して微分可能で,次の式が成り立つ.

 のとき,
のとき,
 を求めてみましょう.
を求めてみましょう.
解

微分法が使いこなせるようになるには,いくつもの問題をこなす必要があります.そこで微分計算に必要な導関数をまとめておきます.








 を求めよう.
を求めよう.
 を求めよう.
を求めよう.