Next: 微分法(Differentiation Formulas) Up: 微分法(DIFFERENTIATION) Previous: 微分法(DIFFERENTIATION) 目次 索引
 とそのグラフ上の点
とそのグラフ上の点
 が与えられたとき,どの直線を点
が与えられたとき,どの直線を点
 における接線とよぶことができるでしょうか.
における接線とよぶことができるでしょうか.
この問題に答えるために,小さな数 を選び,グラフ上に点
を選び,グラフ上に点
 を印します.ここで,この2つの点を通る直線(割線(secant line))を引きます.この状況を記すと次のようになります.
を印します.ここで,この2つの点を通る直線(割線(secant line))を引きます.この状況を記すと次のようになります.
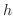 が徐々に右側から0に近づくと,割線は極限位置に近づいていきます.同様に
が徐々に右側から0に近づくと,割線は極限位置に近づいていきます.同様に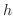 が0に左側から近づくと,割線は右側から近づいたときと同じ極限位置に近づいていきます.この極限位置の直線をグラフ上の点
が0に左側から近づくと,割線は右側から近づいたときと同じ極限位置に近づいていきます.この極限位置の直線をグラフ上の点
 における接線といいます.
における接線といいます.
割線の傾きは


これが,図形を用いた接線の考え方です.
ここからは,このような極限値をもっと系統立てて学んでいきます.
 が
が 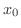 を含むある区間で定義されているとき,極限値
を含むある区間で定義されているとき,極限値

 は,
は,  で微分可能(differentiable) であるといいます.また,この極限値
で微分可能(differentiable) であるといいます.また,この極限値  を点
を点 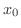 における微分係数といい,
における微分係数といい,
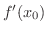 で表わします.
で表わします.
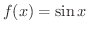 の微分係数
の微分係数
 を求めてみましょう.
を求めてみましょう.
解

 となります.
となります.
これをグラフで見てみましょう.
図2.2を見て下さい.この図には
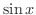 のグラフとその接線(tangent line)
のグラフとその接線(tangent line)  が描かれています.ここで,
が描かれています.ここで, 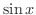 の
の 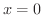 での微分係数と接線
での微分係数と接線  の傾きが同じであることに気付いて下さい.つまり,
の傾きが同じであることに気付いて下さい.つまり,
 は関数
は関数  の
の 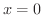 での接線の傾きを表わします.このことから,
での接線の傾きを表わします.このことから,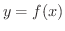 のグラフ上の点
のグラフ上の点
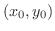 での接線の方程式は,
での接線の方程式は,

となります.また,接線と垂直な線を法線といい,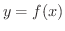 のグラフ上の点
のグラフ上の点
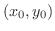 での法線の方程式は,接線と法線は垂直であることから,
での法線の方程式は,接線と法線は垂直であることから,

となります.
 のグラフ上の点
のグラフ上の点 における接線と法線の方程式を求めよ.
における接線と法線の方程式を求めよ.
解
 より,点
より,点 での接線の傾きは
での接線の傾きは
 . したがって,求める接線の方程式は,
. したがって,求める接線の方程式は,



 が
が 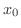 で微分可能でなくても
で微分可能でなくても


 で表わし,後の値を 右側微分係数(right-hand derivative) といい,
で表わし,後の値を 右側微分係数(right-hand derivative) といい,
 で表わします.微分可能の定義より,
で表わします.微分可能の定義より,
 と
と
 が共に存在し,かつ両者が等しいときに限り
が共に存在し,かつ両者が等しいときに限り  は
は  で微分可能となります.
で微分可能となります.
 は
は 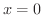 で微分可能か調べてみましょう.
で微分可能か調べてみましょう.
解
まず,
 を求めると
を求めると

 を求めると
を求めると

 は
は 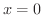 で微分可能ではありません.
で微分可能ではありません.
 は
は 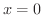 で微分可能ではありませんでしたが,
で微分可能ではありませんでしたが, 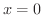 で連続です.微分可能性と連続性の間にはどんな関係があるのでしょうか.
で連続です.微分可能性と連続性の間にはどんな関係があるのでしょうか.
 が
が  で微分可能ならば,
で微分可能ならば,  は
は  で連続である.
で連続である.
証明
 を示せばよいでしょう.そこで
を示せばよいでしょう.そこで

 を
を 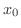 に近づけると
に近づけると

 は
は  で微分可能であることに注意すると
で微分可能であることに注意すると
 |
 |
 |
|
 |
 |

この逆,つまり連続ならば微分可能とはならないことは例題2.1 でみました.では関数が連続で微分可能ではないとき,グラフはどんな形をしているのでしょうか.図2.3を見てみましょう. が
が  で微分可能でないとき,
で微分可能でないとき,
 となっています.これより
となっています.これより
 と
と
 が存在し等しくないときには,関数
が存在し等しくないときには,関数  は
は  でとがっていることが分かります.
でとがっていることが分かります.
関数  が,ある区間Iの各点で微分可能のとき
が,ある区間Iの各点で微分可能のとき  は 区間Iで微分可能(differentiable on I) であるといいます.この場合,区間Iの各点にそこでの微分係数を対応させることにより定まる関数を
は 区間Iで微分可能(differentiable on I) であるといいます.この場合,区間Iの各点にそこでの微分係数を対応させることにより定まる関数を  の 導関数(derivative) といい,
の 導関数(derivative) といい,


 の導関数を求めることを 微分する(differentiate) といいます.
の導関数を求めることを 微分する(differentiate) といいます.
 を微分してみましょう.
を微分してみましょう.
解
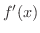 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
![$\displaystyle nx^{n-1} + \lim_{h \rightarrow 0}[\binom{n}{2}x^{n-2}h + \binom{n}{3}x^{n-3}h^2 + \cdots + h^{n-1}] = nx^{n-1}$](img1225.png) |

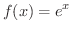 を微分してみましょう.
を微分してみましょう.
解
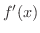 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |

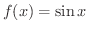 を微分してみましょう.
を微分してみましょう.
解
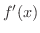 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
![$\displaystyle \lim_{h \rightarrow 0}[\sin{x}\frac{\cos{h} - 1}{h} + \cos{x}\frac{\sin{h}}{h}]$](img1234.png) |
||
 |
 |
||
 |
 例題 例題 参照 参照 |
||
 |
 |

 を微分してみましょう.
を微分してみましょう.
解
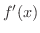 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
![$\displaystyle \lim_{h \rightarrow 0}[\cos{x}\frac{\cos{h} - 1}{h} - \sin{x}\frac{\sin{h}}{h}]$](img1244.png) |
 . また,
. また,
 より,
より,

関数の導関数を,定義に基づいて求めるのは容易ではないことが分かりました.そこで,導関数の計算に必要な公式をまとめておきます.
 が微分可能のとき次式が成り立つ.
が微分可能のとき次式が成り立つ.
 (和の微分法)
(和の微分法)
 (c : 定数)
(c : 定数)
 (積の微分法)
(積の微分法)
 (商の微分法)
(商の微分法)
証明
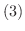 の証明.
の証明.
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
 の導関数を求めてみましょう.
の導関数を求めてみましょう.
解
 |
 |
 |
|
 |
 |
||
 |
 |
 の導関数を求めてみましょう.
の導関数を求めてみましょう.
解
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |

変数  が,ある
が,ある  から
から  まで変化するときの変動量
まで変化するときの変動量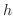 を
を  の 増分(increment) といい,
の 増分(increment) といい,  で表わし,これに対応する
で表わし,これに対応する  の変動量
の変動量
 を
を  の増分といい,
の増分といい,  で表わすと,
で表わすと,
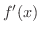 は次のように表わすことができます.
は次のように表わすことができます.


 とは
とは

 が
が  の主要な部分とみなせます.そこで,これを点
の主要な部分とみなせます.そこで,これを点  における関数
における関数 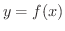 の 微分(differential) といい,
の 微分(differential) といい,  または
または  で表わします.つまり
で表わします.つまり

 のときは,
のときは,
 より
より


 にそれぞれ別々に意味を持たせることができました.
にそれぞれ別々に意味を持たせることができました.
 の微分を求めてみましょう.
の微分を求めてみましょう.
解

 での微分係数を定義に基づいて求めよう.
での微分係数を定義に基づいて求めよう.
 に対応する点における接線の方程式を求めよう.
に対応する点における接線の方程式を求めよう.
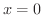 における右側微分係数,および左側微分係数を求めよう.
における右側微分係数,および左側微分係数を求めよう.