Next: *実数の連続性(continium) Up: 関数(FUNCTIONS) Previous: 数列(sequences) 目次 索引
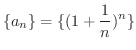 は単調増加数列か調べてみましょう.
は単調増加数列か調べてみましょう.
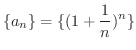 より
より
 |
 |
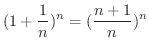 |
|
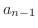 |
 |
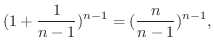 |
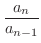 |
 |
![$\displaystyle (\frac{n+1}{n})^{n}(\frac{n-1}{n})^{n-1} = \frac{n}{n-1}[(\frac{n+1}{n})(\frac{n-1}{n})]^n$](img926.png) |
|
 |
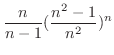 |
||
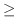 |
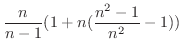 Bernoulliの不等式参照 Bernoulliの不等式参照 |
||
 |
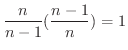 |
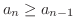 より,
より,  は単調増加であることがわかりました.
は単調増加であることがわかりました.
さてこの数列は収束するのでしょうか.数列の極限値が求められる場合は問題ないのですが,この数列のように何に収束するか,それどころか収束するかどうかもわからない場合があります.そんなとき,次の定理は基本です.
この定理の証明も実数の連続性をもとにしています.証明はこの章の最後で示すことにして,とりあえずこの定理が成り立つことを認めて次の問題を考えてみましょう.
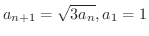 で与えられている数列
で与えられている数列  の極限値を求めてみましょう.
の極限値を求めてみましょう.
解
まず,数列  が収束することを示します.そのためには数列の基礎定理より,
が収束することを示します.そのためには数列の基礎定理より,  が上に有界な単調増加数列か,下に有界な単調減少数列か示せばよいでしょう.
が上に有界な単調増加数列か,下に有界な単調減少数列か示せばよいでしょう.
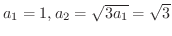 より,
より,
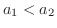 .そこで数学的帰納法を使います.
.そこで数学的帰納法を使います.
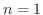 のとき,
のとき,
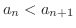 は成り立ちます.次に
は成り立ちます.次に
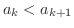 を帰納的仮定とすると,
を帰納的仮定とすると,
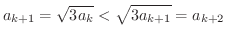
 に対して
に対して
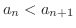 .
.
次に上に有界であることを示します.
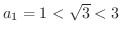
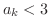 を帰納的仮定とすると,
を帰納的仮定とすると,
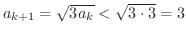 .したがって,すべての自然数
.したがって,すべての自然数  に対して
に対して 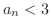 となります.よって
となります.よって  は上に有界な単調増加数列となり
は上に有界な単調増加数列となり  は収束します.
は収束します.
さてこの数列はどんな値に収束するのでしょうか.まず
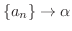 とすると
とすると
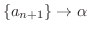 となります.なぜそうなるのか考えてみましょう.
となります.なぜそうなるのか考えてみましょう. は単調増加数列で上に有界なので
は単調増加数列で上に有界なので
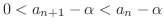
 が
が 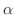 に収束することに注意すると,全ての正の数
に収束することに注意すると,全ての正の数
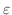 に対して,
に対して, 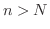 ならば
ならば
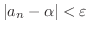 となる自然数
となる自然数 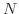 が存在する.よって
が存在する.よって
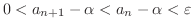
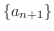 も
も 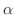 に収束することがわかります.
に収束することがわかります.
次に漸化式
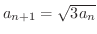 より両辺の極限値を求めると
より両辺の極限値を求めると
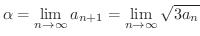
 は
は
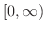 で連続であることに注意すると
で連続であることに注意すると
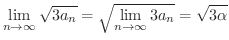
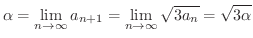
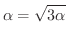
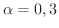 となります.しかし
となります.しかし  は単調増加で
は単調増加で 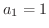 より,
より,
 .したがって,
.したがって,
 となります.
となります.

ちょっと面倒なやり方ですね.そこで漸化式の極限値の求め方には次のようなものがあります.
 に対して
に対して  のとき
のとき
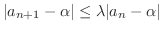
 が存在するならば,
が存在するならば,
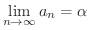
証明
 |
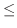 |
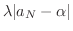 |
|
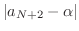 |
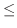 |
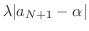 |
|
 |
|||
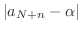 |
 |
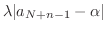 |
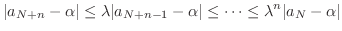
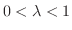 より
より
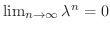 .よって
.よって
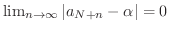 .これより
.これより
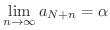
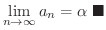
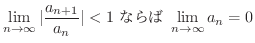
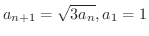 を考えてみましょう.
を考えてみましょう.
解
この定理を用いるには,数列がある値に収束することを仮定しなければなりません.そこで,  が
が 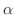 に収束するなら
に収束するなら
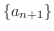 も
も 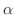 に収束することを用いると
に収束することを用いると
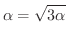
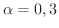 となるけれど
となるけれど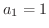 より
より
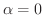 は不可能だとわかります.そこで
は不可能だとわかります.そこで
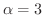 が極限値であることを示しましょう.
が極限値であることを示しましょう.
定理1.6より
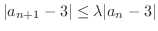 となる
となる
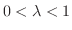 が存在することを示せばよいでしょう.
が存在することを示せばよいでしょう.
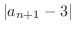 |
 |
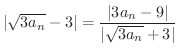 |
|
 |
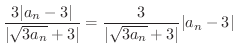 |
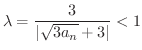 より
より
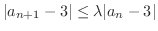

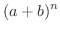 を展開したらどんな形になるのでしょうか.
を展開したらどんな形になるのでしょうか.
解
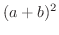 |
 |
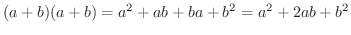 |
|
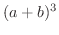 |
 |
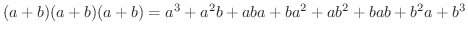 |
|
 |
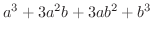 |
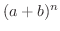 を展開したとき現われる係数は
を展開したとき現われる係数は 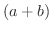 をn回かけたときに現われる
をn回かけたときに現われる
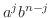 の回数を数えればよいことが分かります.
の回数を数えればよいことが分かります. は全部で
は全部で  個あり,そのうちの
個あり,そのうちの 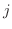 個を使うので,その組み合わせの総数を
個を使うので,その組み合わせの総数を
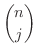 と表わすことにします.
と表わすことにします.
では
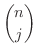 とは何通りなのでしょうか.数えてみましょう.
まず,それぞれの
とは何通りなのでしょうか.数えてみましょう.
まず,それぞれの  に番号を1から
に番号を1から  までつけたとします.そして
までつけたとします.そして  個の
個の  から
から 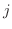 個の
個の  を1つずつとりだして並べると,最初の
を1つずつとりだして並べると,最初の  は
は  個の中のどの
個の中のどの  でもよいので,
でもよいので,  通りの選び方があります.次にくるのは
通りの選び方があります.次にくるのは 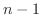 個の中のどの
個の中のどの  でもよいので,
でもよいので, 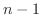 通りの選び方があります.このようにして全部で
通りの選び方があります.このようにして全部で
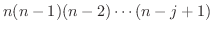 通りあることが分かります.これを
通りあることが分かります.これを
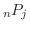 で表わし,
で表わし,  個から
個から 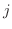 個のもの取り出し順序をつけて並べたときの数,つまり順列の数といいます.しかし,この問題では
個のもの取り出し順序をつけて並べたときの数,つまり順列の数といいます.しかし,この問題では  はすべて同じものと考えられるので,とりだした
はすべて同じものと考えられるので,とりだした 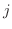 個の
個の  は並び方に関係がありません.そこで
は並び方に関係がありません.そこで
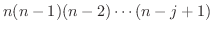 通りのうち
通りのうち の並び方を無視すると
の並び方を無視すると
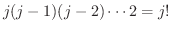 通りの繰り返しがあることが分かります.よって求める組み合わせの総数は
通りの繰り返しがあることが分かります.よって求める組み合わせの総数は
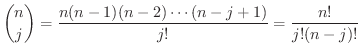
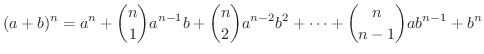
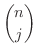 を2項係数といいます.
を2項係数といいます.

さてもう一度数列
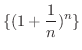 を考えてみましょう.すでにこの数列が単調増加数列であることは示しました.そこで次に上に有界であることを示しましょう.
を考えてみましょう.すでにこの数列が単調増加数列であることは示しました.そこで次に上に有界であることを示しましょう.
そのためには,2項定理を用いて
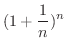 を展開する必要があります.
を展開する必要があります.
 |
 |
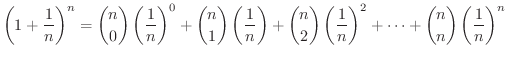 |
|
 |
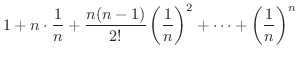 |
||
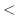 |
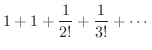 |
||
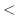 |
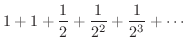 |
||
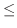 |
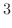 |
 は上に有界な単調増加数列となり数列の基礎定理より収束します.
は上に有界な単調増加数列となり数列の基礎定理より収束します.
さて  の極限値は何でしょうか.この極限値は スイスの数学者 Leonhard Euler (1707-1783) によって初めて定義されたのでEulerの頭文字をとって
の極限値は何でしょうか.この極限値は スイスの数学者 Leonhard Euler (1707-1783) によって初めて定義されたのでEulerの頭文字をとって 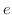 で表わします.つまり
で表わします.つまり
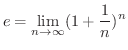
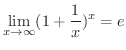 を示してみましょう.
を示してみましょう.
解
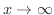 より
より
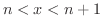 となる
となる  が存在します.よって
が存在します.よって
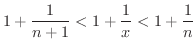
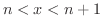 を用いると
を用いると
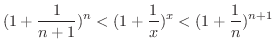
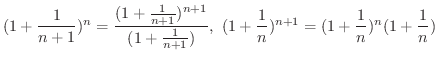
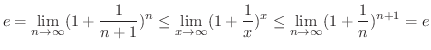
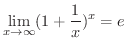

超越関数の定義(definition of transcendental functions)
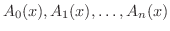 を
を の多項式とするとき,
の多項式とするとき, についての方程式
についての方程式
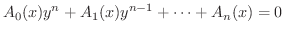
 の関数
の関数 を
を の 代数関数(algebraic function) といい,それ以外の関数を 超越関数(transcendental function) といいます.
の 代数関数(algebraic function) といい,それ以外の関数を 超越関数(transcendental function) といいます.
以前
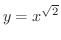 をどう定義したらよいのだろうかという質問をしましたが,いまそれに答えることができます.まず
をどう定義したらよいのだろうかという質問をしましたが,いまそれに答えることができます.まず 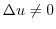 に収束する有理数からなる増加数列
に収束する有理数からなる増加数列
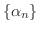 を考えます.例えば,
を考えます.例えば,
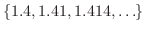
次に, 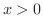 とし,
とし,
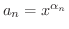 とおくと,
とおくと,
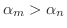 のとき
のとき
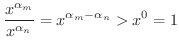
 は増加数列.また
は増加数列.また
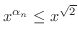 より,
より,  は上に有界な単調増加数列となるので収束します.そこで
は上に有界な単調増加数列となるので収束します.そこで
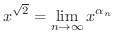
 に収束する有理数列はいくらでもあります.そこで
に収束する有理数列はいくらでもあります.そこで  に収束する別の有理数列
に収束する別の有理数列
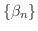 を用いても
を用いても
 が同じ値になることを示す必要があります.このことを数学では 一意性(uniquness) とよんでいます.
が同じ値になることを示す必要があります.このことを数学では 一意性(uniquness) とよんでいます.
 に収束する任意の2つの増加数列を
に収束する任意の2つの増加数列を
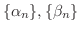 とすると,
とすると,
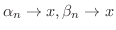 であるので,
であるので,
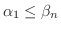 である任意の
である任意の 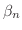 に対して,
に対して,
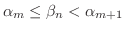 となるような
となるような
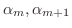 があるはずです(なぜでしょう).まず,
があるはずです(なぜでしょう).まず, 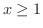 とすると
とすると
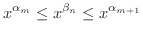
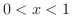 のときは
のときは
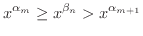
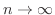 とすると,
とすると,
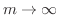 となり,はさみうちの定理より,
となり,はさみうちの定理より,
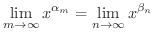
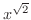 は有理数列
は有理数列
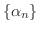 に関係しません.
に関係しません.
一般に 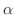 が無理数のとき
が無理数のとき
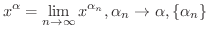 有理数列
有理数列 
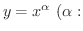 無理数
無理数 の形の関数をベキ関数といいます.
の形の関数をベキ関数といいます.
定義域は
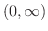 で次の性質が成り立ちます.
で次の性質が成り立ちます.
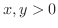 ,任意の実数
,任意の実数
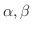 において,次の法則が成り立つ.
において,次の法則が成り立つ.
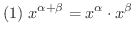
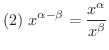
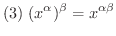
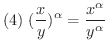
証明
(1)の証明.
 のとき,
のとき,
 とすると,
とすると,
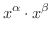 |
 |
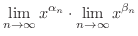 |
|
 |
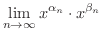 |
||
 |
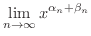 |
||
 |
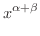 |

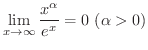 を示してみましょう.
を示してみましょう.
解
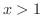 とし,
とし,
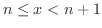 となる自然数を
となる自然数を  とすると,
とすると,
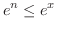
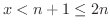 かつ
かつ
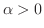 より
より
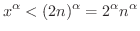
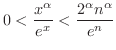
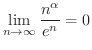 を示しましょう.
を示しましょう.
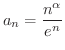 とおくと,
とおくと,
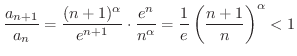
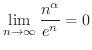
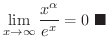
べき関数の定義と同様に,
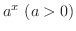 は
は  が無理数
が無理数 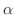 のとき
のとき
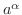 を
を
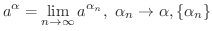 有理数列
有理数列 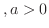
指数関数
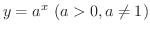 の形の関数を 指数関数(exponential function) といいます.
の形の関数を 指数関数(exponential function) といいます.
定義域は
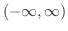 ,値域は
,値域は
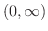 で次の性質をもちます.
で次の性質をもちます.
 ,任意の実数
,任意の実数  において,次のことが成り立つ.
において,次のことが成り立つ.
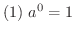
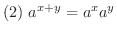
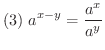
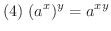
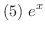 は
は
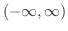 で連続で狭義の単調増加関数
で連続で狭義の単調増加関数
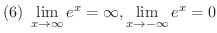
証明
(2)
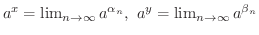 とおくと
とおくと
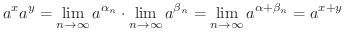

指数関数 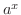 の中でも特に
の中でも特に 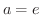 のときは重要です.
のときは重要です.
対数関数
指数関数 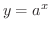 は定義域は
は定義域は
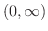 で狭義の単調増加かつ連続です.したがって,逆関数が存在し,それを
で狭義の単調増加かつ連続です.したがって,逆関数が存在し,それを
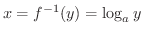 と表わします.中間値の定理より
と表わします.中間値の定理より
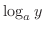 は
は
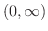 で定義された連続関数になります.この
で定義された連続関数になります.この
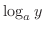 を
を  を底とする対数関数(logarithmic function) といい,
を底とする対数関数(logarithmic function) といい, 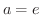 の場合を自然対数といって
の場合を自然対数といって
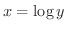 で表わします.
で表わします.
 ,任意の実数
,任意の実数
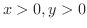 において,次のことが成り立つ.
において,次のことが成り立つ.
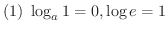
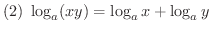
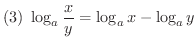
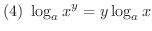
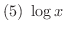 は
は
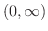 で連続で,単調増加である.
で連続で,単調増加である.
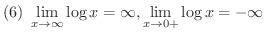
証明
(2)
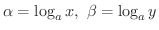 とおくと
とおくと
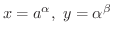 より
より
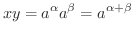
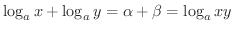

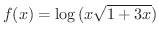 の定義域を求めてみましょう.
の定義域を求めてみましょう.
解
 |
 |
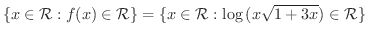 |
|
 |
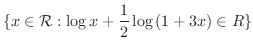 |
||
 |
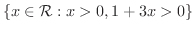 |
||
 |
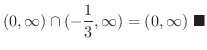 |
双曲線関数
次の関数を 双曲線関数(hyperbolic function) といいます.
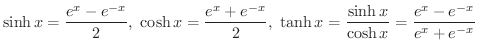
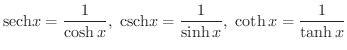
空中に張ったロープを自然にたわませたときにロープが描く曲線のことを 懸垂線 (catenary) といい,この曲線を表わすのに用いられたのが 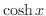 でした.
でした.
|
 の極限値を求めよう.
の極限値を求めよう.
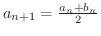 と幾何平均
と幾何平均
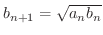 で定義された数列
で定義された数列
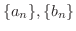 について以下の問に答えよう.
について以下の問に答えよう.
(a)
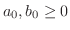 のとき,
のとき, と
と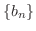 は収束することを示そう.
は収束することを示そう.
(b)
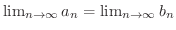 を示そう.この極限値は
を示そう.この極限値は
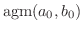 と表される.
と表される.