Next: 数列(sequences) Up: 関数(FUNCTIONS) Previous: 関数の極限(limit of function) 目次 索引
極限
 を考えるときには,
を考えるときには,  は
は 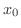 で定義されている必要はありませんでした.また,
で定義されている必要はありませんでした.また,  が
が
 と一致する必要もありませんでした.では極限値とそこでの関数の値が等しいときは,どんなときでしょうか.まず,関数がある点で連続であるということについて考えます.
と一致する必要もありませんでした.では極限値とそこでの関数の値が等しいときは,どんなときでしょうか.まず,関数がある点で連続であるということについて考えます.
 は区間
は区間
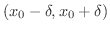 で定義されている.
で定義されている.

 は
は  で連続(continuous) であるという.
で連続(continuous) であるという.
この定義より,関数 の定義域が区間
の定義域が区間
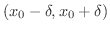 を含んでいるとき,関数
を含んでいるとき,関数 は次の2つの理由を除いて連続です.
は次の2つの理由を除いて連続です.
 が存在しない
が存在しない
 は存在するがその値は
は存在するがその値は と等しくない
と等しくない
1.の場合,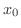 は真性不連続点(essential discontinuity)といい,2の場合は,除去可能な不連続点(removable discontinuity)といいます.つまり,2.の場合は,
は真性不連続点(essential discontinuity)といい,2の場合は,除去可能な不連続点(removable discontinuity)といいます.つまり,2.の場合は, の値を新たに定義することにより,
の値を新たに定義することにより,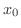 で連続にすることができるということです.
で連続にすることができるということです.
ここで,1.の条件を調べるのに便利なものがあります.
右側極限値,左側極限値(right-hand limit, left-hand limit)
 を
を 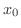 に近づけるとき,特に
に近づけるとき,特に  という制限があるときには,
という制限があるときには,  は
は 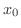 より小さい値をとりながら
より小さい値をとりながら 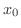 に近づくので,これを
に近づくので,これを
 または
または
 と表わします.同様に,
と表わします.同様に,  が
が 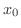 より大きい値をとりながら,
より大きい値をとりながら, 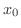 に近づくとき,これを
に近づくとき,これを
 または
または
 と表わします.
と表わします.
 のときに,
のときに,  がある定数
がある定数 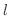 に限りなく近づくことを
に限りなく近づくことを
 または
または
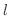 を
を  の
の 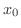 における左側極限値(left-hand limit) といいます.同様に,
における左側極限値(left-hand limit) といいます.同様に,
 のときに,
のときに,  がある定数
がある定数 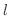 に限りなく近づくことを
に限りなく近づくことを
 または
または
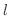 を
を  の
の 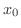 における右側極限値(right-hand limit) といいます.
における右側極限値(right-hand limit) といいます.
 の
の 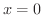 における右側極限値と左側極限値を求めてみましょう.
における右側極限値と左側極限値を求めてみましょう.
解
 が左側から0 に近づくと,
が左側から0 に近づくと,  は常に0より小さいので
は常に0より小さいので  .よって
.よって
 となります.つまり,
となります.つまり,

 が右側から0 に近づくと,
が右側から0 に近づくと,  は常に0より大きいので
は常に0より大きいので 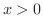 .よって
.よって
 となります.つまり,
となります.つまり,


ここまでの極限値の問題には常に極限値が存在しました.しかし極限値はいつも存在するのでしょうか.もし存在しないのなら,どうやってそのことを説明したらいいのでしょうか.そんな質問に次の定理は答えてくれます.
 とは
とは
 かつ
かつ
 ということと同値である.
ということと同値である.
証明 各自に任せます.
この定理より
 と
と
 が存在し,かつ等しいときに限り
が存在し,かつ等しいときに限り  の極限値が存在するといえます.つまりそれ以外の場合には極限値が存在しません.
の極限値が存在するといえます.つまりそれ以外の場合には極限値が存在しません.
 を求めてみましょう.
を求めてみましょう.
解


 は存在しません.
は存在しません.

 が
が 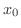 に限りなく近づくとき,
に限りなく近づくとき,  の値が限りなく大きくなる場合には,
の値が限りなく大きくなる場合には,

 が
が 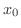 に限りなく近づくとき,
に限りなく近づくとき,  の値が負となりその絶対値が限りなく大きくなる場合には,
の値が負となりその絶対値が限りなく大きくなる場合には,

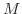 が与えられても,
が与えられても,  がある実数
がある実数 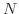 より大きいとき,
より大きいとき,  となるということです.
となるということです.
また,  が限りなく大きくなるとき,
が限りなく大きくなるとき,  の値が
の値が 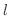 に限りなく近づくならば,
に限りなく近づくならば,

 は
は  で連続か考えてみましょう.
で連続か考えてみましょう.
解
極限値は
 また
また  より
より
 となります.よって
となります.よって  は
は  で不連続です.グラフを想像してみると,
で不連続です.グラフを想像してみると,  において
において  の値がジャンプしています.
の値がジャンプしています.

 は
は 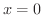 で連続か調べてみましょう.
で連続か調べてみましょう.
解 まず,


 )より
)より

 より
より  は
は 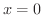 で連続だということがわかります.
で連続だということがわかります.

関数  が
が  の片側だけで定義されている場合には,上の定義は当てはまりません.そこで,
の片側だけで定義されている場合には,上の定義は当てはまりません.そこで,

 は
は  で左側連続(continuous from the left) であるといいます.同様に,
で左側連続(continuous from the left) であるといいます.同様に,

 は
は  で右側連続(continuous from the right) であるといいます.また,
で右側連続(continuous from the right) であるといいます.また,  が区間 Iのどの点でも連続であるとき,
が区間 Iのどの点でも連続であるとき,  は区間Iで連続であるといいます.例えば,整式,
は区間Iで連続であるといいます.例えば,整式,
 は区間
は区間
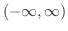 で連続です.また,有理関数は分母が 0 になる点を除いたすべての区間で連続です.
で連続です.また,有理関数は分母が 0 になる点を除いたすべての区間で連続です.
次に連続な関数は,四則の演算を行ってもまた連続であるというすばらしい性質を持っています.
 と
と 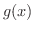 が
が  で連続であるとすると
で連続であるとすると
 も
も  で連続である
で連続である
 も
も  で連続である.ただし,
で連続である.ただし, 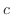 は定数
は定数
 も
も  で連続である
で連続である
 も
も  で連続である.ただし,
で連続である.ただし,

証明
(1)
 より
より


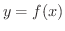 が
が  で連続で,
で連続で, が
が
 で連続ならば,合成関数
で連続ならば,合成関数
 も
も  で連続である.
で連続である.
証明


これらのことから分かるように連続な関数は非常に扱いやすい関数です.
 は
は  で連続であることを示してみましょう.
で連続であることを示してみましょう.
解
まず,
 は
は  と
と
 の合成関数と考えられ,
の合成関数と考えられ,  と
と
 はすべての
はすべての  と
と  で連続なので,この定理より
で連続なので,この定理より
 は
は  で連続です.また
で連続です.また  は
は
 で連続なので定理1.4より
で連続なので定理1.4より  で
で
 は連続となります.
は連続となります.

次に連続関数の基本的性質を表わすものとして,中間値の定理(intermediate theorem) と最大・最小値の定理(max-min theorem) とよばれる2つの定理を考えてみましょう.
 が閉区間
が閉区間 ![$[a,b]$](img158.png) で連続ならば,
で連続ならば,
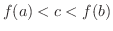 である任意の
である任意の 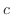 に対して,
に対して,
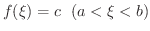
 が存在する.
が存在する.
 が閉区間
が閉区間 ![$[a,b]$](img158.png) で連続ならば,この区間に
で連続ならば,この区間に  が最大値をとる点,および最小値をとる点が存在する.
が最大値をとる点,および最小値をとる点が存在する.
上の定理にでてきた最大値をとるとはどういうことか確認しておきましょう.
関数  が区間
が区間 ![$[a,b]$](img158.png) で最大値をとるとは,次の2つの条件が共に成り立つということです.
で最大値をとるとは,次の2つの条件が共に成り立つということです.
![$x \in [a,b]$](img704.png) に対して,
に対して,
 となる
となる 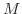 が存在する.
が存在する.
 となる
となる  が
が ![$[a,b]$](img158.png) 内に存在する.
内に存在する.
この2つの定理がどんなことをいっているのか考えてみましょう.
まず連続関数のグラフは2点
 を結ぶつながった曲線で表わされると認めれば,図の上からは明らかでしょう.しかし,連続関数は本当につながった曲線で表わせるのでしょうか.この問題は実数の連続性を基にして初めて証明することができるのです.実数の連続性とは,簡単にいうと実数を大小の順序に並べたとき,実数はどこにも切れめなくぎっしりと並んでいるということです.そこで証明は1.7節にまかせることにして,ここでは実数の連続性を認めたとして話を進めましょう.つまり,連続関数のグラフはつながった曲線で表せると考えます.
を結ぶつながった曲線で表わされると認めれば,図の上からは明らかでしょう.しかし,連続関数は本当につながった曲線で表わせるのでしょうか.この問題は実数の連続性を基にして初めて証明することができるのです.実数の連続性とは,簡単にいうと実数を大小の順序に並べたとき,実数はどこにも切れめなくぎっしりと並んでいるということです.そこで証明は1.7節にまかせることにして,ここでは実数の連続性を認めたとして話を進めましょう.つまり,連続関数のグラフはつながった曲線で表せると考えます.
 は少なくとも
は少なくとも 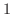 つの実数解を持つことを示しましょう.
つの実数解を持つことを示しましょう.
解
まず,方程式が解を持つとは,方程式を表わす曲線のグラフが  軸と共有点を持つということと同じだということを理解してください.つまり曲線のグラフが
軸と共有点を持つということと同じだということを理解してください.つまり曲線のグラフが  軸に接するか横切ればよいのです.そこで
軸に接するか横切ればよいのです.そこで
 とおき,
とおき,  が負の値と正の値をとるような
が負の値と正の値をとるような  の値を適当にとります.例えば,
の値を適当にとります.例えば,  と
と  を計算すると
を計算すると

 は
は ![$[-2,1]$](img713.png) で連続なので,点
で連続なので,点  と点
と点  を曲線で結びます.するとどんなふうに結んでも,必ず
を曲線で結びます.するとどんなふうに結んでも,必ず  軸と共有点を持つ点があることが,中間値の定理により保証されます.そこでこの点を
軸と共有点を持つ点があることが,中間値の定理により保証されます.そこでこの点を  とおくと,
とおくと,
 .つまりこの
.つまりこの  が
が
 の実数解になります.
の実数解になります.

ここで重要なのは解が存在することであって,解はどこにあるかではないのです.つまり,解の存在を示すには3次方程式を解く必要はないのです.
関数 が区間
が区間![$[a,b]$](img158.png) で連続で,
で連続で,
 または
または
 のとき,中間値の定理より,方程式
のとき,中間値の定理より,方程式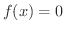 は少なくとも1つの解を区間
は少なくとも1つの解を区間![$[a,b]$](img158.png) 内に持っていることを知っています.話を簡単にするために,解は1つしか無いことにします.さて,どうやって解を求めるのでしょうか.この問題を解くための,最も簡単な方法の1つに2分法(bisection method)とよばれる方法があります.
内に持っていることを知っています.話を簡単にするために,解は1つしか無いことにします.さて,どうやって解を求めるのでしょうか.この問題を解くための,最も簡単な方法の1つに2分法(bisection method)とよばれる方法があります.
2分法 まず区間![$[a,b]$](img158.png) を2等分します.もし,解
を2等分します.もし,解 が中点でなければ,解
が中点でなければ,解 は必ず2つに分けられた区間のどちらかに属しているはずです。そこで,
は必ず2つに分けられた区間のどちらかに属しているはずです。そこで,
![$f(a),f([a+b]/2),f(b)$](img720.png) の符号を調べ,
の符号を調べ, がどちらに属しているか見つけます.見つけたら,
がどちらに属しているか見つけます.見つけたら, が含まれる区間をまた2等分し,解
が含まれる区間をまた2等分し,解 が中点でなければ,解
が中点でなければ,解 がどちらの区間にあるか見つけます.これの繰り返しによって,やがて
がどちらの区間にあるか見つけます.これの繰り返しによって,やがて に十分近い値を求めることができます。
に十分近い値を求めることができます。
では,こうやって求めた近似値が真値にどのくらい近い値か調べてみます.まず,区間![$[a,b]$](img158.png) を1回2分すると,区間の幅はもとの半分になります.したがって,
を1回2分すると,区間の幅はもとの半分になります.したがって, 回,2等分を行なうと,区間の幅は
回,2等分を行なうと,区間の幅は


 の近似値を区間
の近似値を区間![$[1,2]$](img724.png) において誤差
において誤差 以内で求めよう.
以内で求めよう.
解 まず,誤差が 以内になるまでに2分法を何回用いるか計算してみましょう.
以内になるまでに2分法を何回用いるか計算してみましょう.

 . この不等式を解くと,
. この不等式を解くと, となります.したがって,2分法を4回繰り返せば十分です.
となります.したがって,2分法を4回繰り返せば十分です.

 を近似値とすると,真値
を近似値とすると,真値
 と誤差
と誤差 以内であることが分かります.
以内であることが分かります.

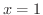 で連続になるように,
で連続になるように, を定義しよう.
を定義しよう.
 の近似値を区間
の近似値を区間![$[0,1]$](img747.png) において誤差
において誤差 以内で求めよう.
以内で求めよう.
 は
は  で連続か調べよう.
で連続か調べよう.
 は区間
は区間
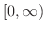 で連続であることを示そう.
で連続であることを示そう.
 は
は
 内に実数解を持つことを証明しよう.
内に実数解を持つことを証明しよう.