内積(Inner product)

空間のベクトルにおいて次の3つのことは基本です．(1)和, (2)スカラー倍, (3)内積(スカラー積)．

和とスカラー倍については、すでに学んだので、ここでは空間のベクトルの内積について紹介します。

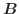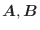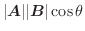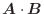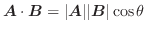0でないベクトル $\boldsymbol{A}, \boldsymbol{B}$ とそれらのなす角を $\theta(0 \leq \theta \leq \pi)$ とします．このとき, 実数 $\vert\boldsymbol{A}\vert\vert\boldsymbol{B}\vert\cos{\theta}$ を $\boldsymbol{A}$ と $\boldsymbol{B}$ の内積(dot product)またはスカラー積といい 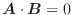$\boldsymbol{A} \cdot\boldsymbol{B}$ と表します．つまり

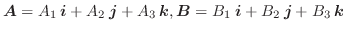
$\displaystyle \boldsymbol{A} \cdot\boldsymbol{B} = \vert\boldsymbol{A}\vert\vert\boldsymbol{B}\vert\cos{\theta}$

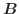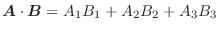$\boldsymbol{A}, \boldsymbol{B}$ のうち少なくとも一方が0のときは, $\boldsymbol{A} \cdot\boldsymbol{B} = 0$ と定めます．

定理 1..1

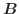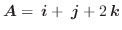2つのベクトル $\boldsymbol{A}, \boldsymbol{B}$ に対して， $\boldsymbol{A} = A_{1}\:\boldsymbol{i} + A_{2}\:\boldsymbol{j} + A_{3}\:\boldsy... ...mbol{B} = B_{1}\:\boldsymbol{i} + B_{2}\:\boldsymbol{j} + B_{3}\:\boldsymbol{k}$ ならば，

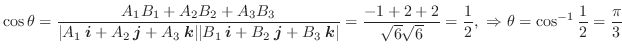
$\displaystyle \boldsymbol{A} \cdot\boldsymbol{B} = A_{1}B_{1} + A_{2}B_{2} + A_{3}B_{3}$

である．

問 1..2

内積の定義と余弦定理を用いて，上記の定理を証明せよ．

例題 1..2

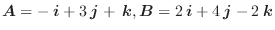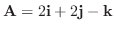$\boldsymbol{A} = \:\boldsymbol{i} + \:\boldsymbol{j} + 2\:\boldsymbol{k}$ と $\boldsymbol{B} = -\:\boldsymbol{i} + 2\:\boldsymbol{j} + \:\boldsymbol{k}$ のなす角を求めよ．解

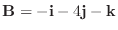
$\displaystyle \cos{\theta} = \frac{A_{1}B_{1} + A_{2}B_{2} + A_{3}B_{3}}{\vert ... ...}} = \frac{1}{2}, \Rightarrow \theta = \cos^{-1}{\frac{1}{2}} = \frac{\pi}{3}$

問 1..3

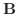$\boldsymbol{A} = -\:\boldsymbol{i} + 3\:\boldsymbol{j} + \:\boldsymbol{k}, \boldsymbol{B} = 2\:\boldsymbol{i} + 4\:\boldsymbol{j} - 2\:\boldsymbol{k}$ について, 次の値を求めよ．

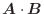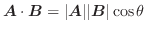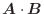(1) $\boldsymbol{A}$ と $\boldsymbol{B}$ のなす角 (2) $\boldsymbol{A}$ 方向の単位ベクトル(単位ベクトルは大きさが1のベクトル)

演習問題1.2

1.: $\boldsymbol{A} = -\:\boldsymbol{i} + 3\:\boldsymbol{j} + \:\boldsymbol{k}, \boldsymbol{B} = 2\:\boldsymbol{i} + 4\:\boldsymbol{j} - 2\:\boldsymbol{k}$ とするとき，次の質問に答えよ．
(1): $\boldsymbol{A}$ と $\boldsymbol{B}$ のなす角
(2): $\boldsymbol{A}$ 方向への単位ベクトル．
2.: ${\bf A}= 2{\bf i} + 2{\bf j} - {\bf k}$ と ${\bf B} = -{\bf i} -4{\bf j} - {\bf k}$ とするとき，次の質問に答えよ．
(1): ${\bf A}$ と ${\bf B}$ の内積
(2): ${\bf A}$ と ${\bf B}$ のなす角