空間のベクトル(Vector in space)

平面や空間での有向線分によって表されるベクトルにはすでに出会ったことがあるでしょう．ここでは, 3次元空間において有向線分で表されるベクトルを 空間のベクトル とよびます．空間のベクトルは, 方向と大きさをもつ線分を表します．

これから先, 空間のベクトルはいつも有向線分で表されます．空間のベクトルは, 皆さんが今まで扱ってきた数と違い, 同じ方向と大きさをもちさえすれば等しいということができます．つまり, どの空間のベクトルもそれに平行で大きさが同じ空間のベクトルで置き換えても等しく, このことから, 空間のベクトルは方向と大きさを変えないで自由に動かすことができます．

初めに, ふたつの初等的な演算, 加法(vector addition)およびスカラー乗法(scalar multiplication)を空間のベクトルに対して定義します．ベクトルの和を作る操作を加法といい, ベクトルを定数倍することをスカラー乗法といいます．

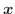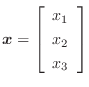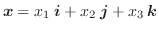空間のベクトル $\boldsymbol{x}$に対して、直交座標を用意し、始点が原点になるように平行移動したとき、原点と終点の座標 $(x_{1}, x_{2},x_{3})$を結ぶベクトルを $\boldsymbol{x} = \left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]$または， ${}^t[x_{1} x_{2} x_{3}]$と表します．特に$xyz$-空間を扱う場合には，原点を始点とし点 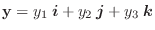$(1,0,0),(0,1,0),(0,0,1)$を結んでできるベクトル 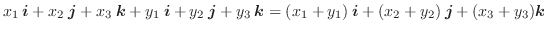$\boldsymbol{i},\:\boldsymbol{j},\:\boldsymbol{k}$を用いて， ${\bf x} = x_{1}\:\boldsymbol{i} + x_{2}\:\boldsymbol{j} + x_{3}\:\boldsymbol{k}$ 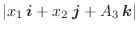と表します．すると、２つのベクトル 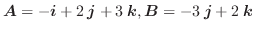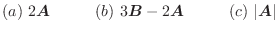$\boldsymbol{x} = x_{1}\:\boldsymbol{i} + x_{2}\:\boldsymbol{j} + x_{3}\:\boldsymbol{k}$， ${\mathbf y} = y_{1}\:\boldsymbol{i}+ y_{2}\:\boldsymbol{j} + y_{3}\:\boldsymbol{k}$の和は、

$$x_{1}\:\boldsymbol{i} + x_{2}\:\boldsymbol{j} + x_{3}\:\boldsymbo... ...:\boldsymbol{i} + (x_{2}+y_{2})\:\boldsymbol{j} + (x_{3} + y_{3})\boldsymbol{k}$$

と定義することができます.

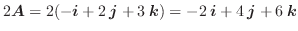
また，ベクトルの大きさ 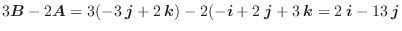$\vert x_{1}\:\boldsymbol{i} + x_{2}\: \boldsymbol{j} + A_{3}\:\boldsymbol{k}\vert$ は, 原点と点 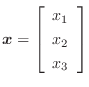$(x_{1}, x_{2},x_{3})$ を結ぶ線分の距離となり, 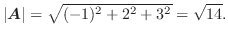$\sqrt{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}$ で表せます．

例題 1..1  

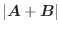$\boldsymbol{A} = -\boldsymbol{i} + 2\:\boldsymbol{j} + 3\:\boldsymbol{k}, \boldsymbol{B} = -3\:\boldsymbol{j} + 2\:\boldsymbol{k}$ について, 次の値を求めよ．

$$(a) 2\boldsymbol{A} \hskip 1cm (b) 3\boldsymbol{B} - 2\boldsymbol{A} \hskip 1cm (c) \vert\boldsymbol{A}\vert$$

解 (a) $2\boldsymbol{A} = 2(-\boldsymbol{i} + 2\:\boldsymbol{j} + 3\:\boldsymbol{k}) = -2\:\boldsymbol{i} + 4\:\boldsymbol{j} + 6\:\boldsymbol{k}$.
(b) $3\boldsymbol{B} - 2\boldsymbol{A} = 3(-3\:\boldsymbol{j} + 2\:\boldsymbol{k}) -... ...+ 2\:\boldsymbol{j} + 3\:\boldsymbol{k} = 2\:\boldsymbol{i} -13\:\boldsymbol{j}$.
(c) $\vert\boldsymbol{A}\vert = \sqrt{(-1)^2 + 2^2 + 3^2} = \sqrt{14}.$

問 1..1  

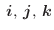
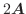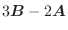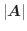
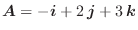上の例題において $\vert\boldsymbol{A} + \boldsymbol{B}\vert$を求めよ.

基本ベクトル

原点と点 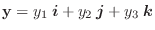$(1,0,0),(0,1,0),(0,0,1)$を結んでできるベクトル 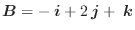$\:\boldsymbol{i},\:\boldsymbol{j},\:\boldsymbol{k}$を直交座標系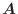$(O-xyz)$における基本ベクトルといいます．また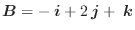， $\:\boldsymbol{i},\:\boldsymbol{j},\:\boldsymbol{k}$のように大きさが1のベクトルを 単位ベクトル(unit vector) といいます．

演習問題1.1

1.

$\boldsymbol{A} = -\boldsymbol{i} + 2\:\boldsymbol{j} + 3\:\boldsymbol{k}, \boldsymbol{B} = -3\:\boldsymbol{j} + 2\:\boldsymbol{k}$のとき，次の値を求めよ．

(1)

$2\boldsymbol{A}$

(2)

$3\boldsymbol{B} - 2\boldsymbol{A}$

(3)

$\vert\boldsymbol{A}\vert$

(4)

$\vert\boldsymbol{A} + \boldsymbol{B}\vert$

2.

$\boldsymbol{A} = -\boldsymbol{i} + 2\:\boldsymbol{j} + 3\:\boldsymbol{k}$ and $\boldsymbol{B} = -\:\boldsymbol{i} + 2\:\boldsymbol{j} + \:\boldsymbol{k}$とするとき，次の値を求めよ．

(1)

$\boldsymbol{A}$ + $\boldsymbol{B}$

(2)

Angle between $\boldsymbol{A}$ and $\boldsymbol{B}$