Next: 連続型確率分布(continuous probability distribution) Up: 確率分布 Previous: 確率分布(probability distribution) 目次 索引
確率変数 のとる値を
のとる値を
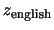 とし,各事象
とし,各事象
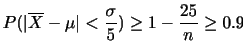 の確率を
の確率を
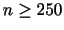 とするとき,
とするとき,
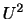
 の確率分布
の確率分布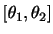 は
は
Xの値 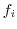 |
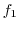 |
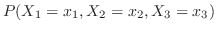 |
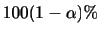 |
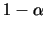 |
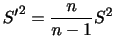 |
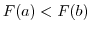 |
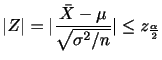 |
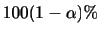 |
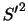 |
 のとる値を
のとる値を
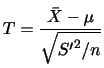 とするとき,その分布関数
とするとき,その分布関数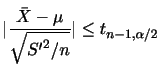 は次のように求められる.
は次のように求められる.
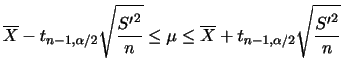
確率分布 と分布関数
と分布関数 は次の性質をもつ.
は次の性質をもつ.
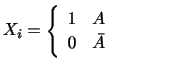
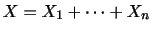
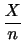
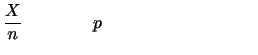
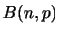
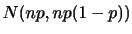
平均と分散
確率変数 の平均(期待値)と分散は次の式で定義されます.
の平均(期待値)と分散は次の式で定義されます.
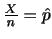
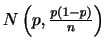
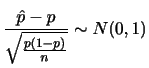 のとき,
のとき,
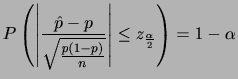
解答
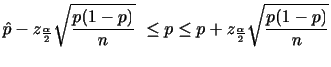 を
を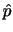 で表すと
で表すと
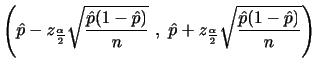
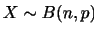 |
 |
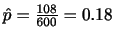 |
|
 |
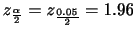 |
||
 |
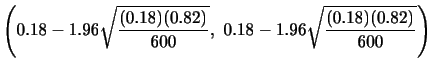 |
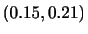 が成り立つことを示そう.
が成り立つことを示そう.
解答
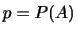 |
 |
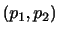 |
|
 |
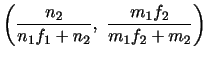 |
||
 |
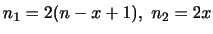 |