Next: 離散型確率分布(descrete probability distribution) Up: 確率分布 Previous: 確率の定義(definition of probabilty) 目次 索引
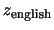 なる
なる 個の値をとる変数
個の値をとる変数 に対して,
に対して,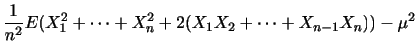 なる確率
なる確率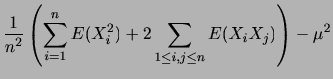 が与えれているとき,
が与えれているとき, を確率変数といいます.
を確率変数といいます.
 とそれに対応する確率
とそれに対応する確率
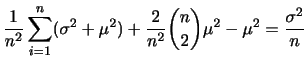 との対応関係を確率分布といいます.
との対応関係を確率分布といいます.
 の値がある値
の値がある値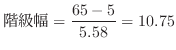 までとる確率を
までとる確率を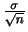 で表し,確率変数
で表し,確率変数 の分布関数といいます.つまり,分布関数は
の分布関数といいます.つまり,分布関数は
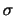 で与えられます.
で与えられます.
サイコロを6回投げるとき,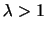 「1の目がでる」という事象のおきる確率は
「1の目がでる」という事象のおきる確率は
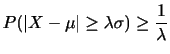 で与えられる.このとき,
で与えられる.このとき,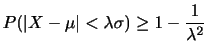 「事象
「事象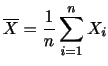 が発生する回数」とおくと,
が発生する回数」とおくと, は0から6までの7個の値をとる変数で,
は0から6までの7個の値をとる変数で,
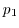
 は確率変数で,その確率分布は2項分布(binomial distribution)とよばれ,
は確率変数で,その確率分布は2項分布(binomial distribution)とよばれ,
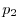 と表します.
と表します.
次の1〜3を満たす試行をベルヌーイ試行といいます.
1回の試行において,ある事象 が発生する確率を
が発生する確率を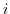 とします.
とします. 回のベルヌーイ試行列において,ちょうど
回のベルヌーイ試行列において,ちょうど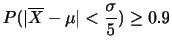 回事象
回事象 が発生する確率は
が発生する確率は
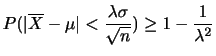
 の確率分布を2項分布といい,
の確率分布を2項分布といい,
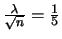 と表します.
と表します.
確率変数 のとる値が有限個または,無限個であっても自然数で番号が付けられる場合,確率変数
のとる値が有限個または,無限個であっても自然数で番号が付けられる場合,確率変数 は離散型であるという.また,確率変数
は離散型であるという.また,確率変数 がある区間内の全ての実数を取り得る場合,連続型であるという.
がある区間内の全ての実数を取り得る場合,連続型であるという.