Next: 正規分布(normal distribution) Up: 確率分布 Previous: 離散型確率分布(descrete probability distribution) 目次 索引
連続変量の確率分布において,任意の定数
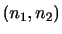 に対して,確率
に対して,確率
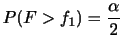 が
が
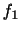
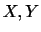 が
が
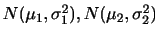 で存在するとき,この
で存在するとき,この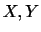 を,この確率分布の確率密度関数(probability density function)といいます.また,確率密度関数は次の性質を持っています.
を,この確率分布の確率密度関数(probability density function)といいます.また,確率密度関数は次の性質を持っています.
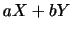
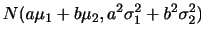
確率分布
確率変数 が区間
が区間
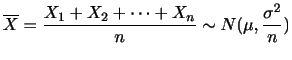 にある確率が
にある確率が
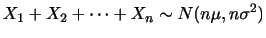
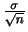 を,確率変数
を,確率変数 の確率分布(probability distribution)といいます.
の確率分布(probability distribution)といいます.
平均と分散
確率変数 の平均(期待値)と分散は次の式で定義されます.
の平均(期待値)と分散は次の式で定義されます.